I assume here that the price evolution is modelised by a
Fractional Brownian Motion (FBM) of index-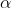
(0<
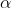
<1): href="http://www.codecogs.com/">
\rightarrow&space;\mathbb{R})
where X(t) represents the price at time t, so that we have the following equality (E1) about the expectation of dependent price increments (demonstration in [FALC03]pp267-268):
![E[(X(t)-X(0))(X(t+h)-X(t))]=\frac{1}{2}[(t+h)^{2\alpha }-t^{2\alpha }-h^{2\alpha }]](http://www.codecogs.com/gif.latex?E[(X(t)-X(0))(X(t+h)-X(t))]=\frac{1}{2}[(t+h)^{2\alpha&space;}-t^{2\alpha&space;}-h^{2\alpha&space;}])
Clearly the value
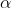
=1/2 seems to play a very specific role in that equation, since it cancels out its right-side term.
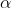
=1/2 indeed consists in the classical Brownian Motion (Wiener Brownian Motion:WBM) where the increments over time of the variable X are independent.
This index
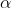
is directly linked to the Fractal Dimension D
f by the relation:
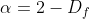
Therefore, when
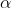
=1/2, which is happening when D
f=1.5, we have a genuine Random Walk.
When such is not the case, however, we can say:
1)
Df<1.5
This case is equivalent to
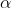
>1/2, and we can then expect from the equality (E1) that X(t+h)-X(t) tend to be of the same sign as X(t)-X(0), therefore, if X(t) has an history of increasing, the next move X(t+h) will be more likely to be up, similarly if X(t) has an history of decreasing, the next move will tend to be down. In this case,
we are in a trend.
2)
Df>1.5
This case is equivalent to 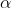<1/2.> In this case, X(t+h)-X(t) tend to be of the opposite sign of X(t)-X(0), therefore, following the same logic as above, we are in a trend reversal period.
No comments:
Post a Comment