Rescaled Range Analysis

The Rescaled Range Analysis is an interesting statistical tool to detect long-range dependence in a time-series, and it also provides a method to estimate the Hurst Exponent. I have detailed to some extent this method on my other blog at this address.

Having estimated the Hurst Exponent, I was then able to write a Fractalised Moving Average, very much in the style of the FRASMA, except that this one, called RS_FRASMA, used the estimation of the Hurst Exponent coming from a Rescaled Range Analysis.
Unfortunately, this analysis is rather demanding in terms of computing power and time, I was therefore limited to small sample of values and even then, the processing time is quite long, furthermore, the result of the estimation is not very good, and not good enough anyway to be usable in terms of a fractional bands type of indicator.
Nevertheless, the RS_FRASMA may still be of some interest, if only in comparison with other MAs, and I therefore uploaded a script in MQL4 at this address.

The logic of the RS_FRASMA is similar to the one at work in the FRASMA: An SMA is modified by multiplication of its speed with a factor alpha defined as such:



Where H is the Hurst Exponent.

Here is what it looks like, the red curve is the RS_FRASMA, the yellow one is the FRASMA, and the blue one is an SMA, all with unmodified speed of 30:



The parameters of RS_FRASMA are:
period (integer): The size of the sample on which the Rescaled Range Analysis is performed, it must be a power of 2 (4,8,16,32,64,128,...), the default is 64, and in consideration of the limited computing power of MT4, I don't advise going higher than 256.
normal_speed (integer): This is the normal speed of the Moving Average before it is modified by the Hurst Parameter.
PIP_Convertor (integer): The factor necessary to convert real price to PIPS, default is 10000 (for EUR/USD)
type_data (0,1,2,3,4,5 or 6): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW, 4=MEDIAN, 5=TYPICAL, 6=WEIGHTED), default is 0.

EUR/USD outlook

Technically, the EUR/USD may have reached its top as the 61.8% fibonacci retracement of the range 1.6040/1.2329 at 1.4842 (even though the key resistance is 1.4867) and could now go for a dip back into the 1.2s (albeit some resistance on the way).

On the fundamental side, the EUR is again now over-valued. Besides, in a recent report, the OECD wrote:

"The reform of global exchange rate regimes and the dollar reserve currency problem is extremely important, but is also unlikely to be achieved any time soon." From The Financial Crisis and the Requirements of Reform - Adrian Blundell-Wignall

The USD is therefore strengthened in its position as a reserve currency in the medium term.
In terms of financial regulations, the G20 has clearly achieved nothing but a bunch of populistic tricks that will have no consequence whatsoever, and as explained in the OECD report, this should lead to a sluggish recovery, especially in Europe and USA.
In this context, the recent rise of the EUR, upshot of an early enthusiasm, should be short-lived, as the reality of national deficits, progressing unemployment, limited credit and falling consumption will set in.

Some general updates and a comment on FRASMA

Let me apologize for a rather long silence, I've been studying some more fundamental problems that require me to revamp and improve a bit my knowledge on various mathematics topics.
I shall try to resume posting more frequently whenever I find something interesting, and anyway, I should at least be able to post some more basic stuff after summer.

Meanwhile, some people left a few comments on the MQL4 community, particularly on the thread concerning FRASMA that may be of interest for those using this moving average.

Blogs dynamics

As some of you may have noticed, from now on, I will publish all the posts that do not relate directly to trading or economics on two other blogs: http://thenomadicchronicle.blogspot.com/ for english, and http://chroniquenomade.blogspot.com/ for french (one will not necessarily be the translation of the other, the content may be different)
The posts which are directly focusing on mathematics will also be made on another blog: http://stochasticfractals.wordpress.com/

I however leave all past posts on this blog.
This is not to mean that my posts on the other blogs will not relate in anyway to trading, I actually believe that most of them, if not all, do relate to it in some ways. My intention in separating them is only for the purpose of clarity.

Internationalization of the Yuan

Today, the Bank of China Chairman Xiao Gang announced the beginning of a scheme to internationalize the Chinese Yuan. The immediate real effect of this declaration will be relatively mild, this internationalization will only concern trading relationships with south-east asian countries, but we can expect a psychological effect on the exchange rate of the Yuan, and therefore a trade shorting USD against the CNY seems possible.

On a more fundamental point of view, the Yuan is still very far from being a reserve currency, but given the geopolitical situation, and the weakening of US economy, the environment is certainly propitious for China to undertake such measures in the direction of a strengthening of the Yuan and basically an affirmation of its real weight in the world economy. Clearly, until now, China has been relying on US consumption to boost its economy, with this consumption currently falling (and still far from bottoming), China would be well-inspired to develop its domestic consumption and that supposes a strengthening of the Yuan.

For more details, see Reuters, insiderNews,...etc.

Fractional Bands

Let's consider again the equation (1) from yesterday:



We were facing the technical problem of having very small real variations of prices, leading to very small standard deviations. This can however be easily solved by converting all our values in PIPS. For EUR/USD, it simply consists in multiplying all the prices by 10000. If we then apply the above equation to PIPS, and convert it back to the scale of real prices (by dividing by 10000), we can then get a proper representation of bands, which, given that they are strictly obeying the model of FBM we are working with, I shall name Fractional Bands.

Here is a representation of these fractional bands for the 5 mn timeframe of EUR/USD, the red bands are the Fractal Bands defined as earlier, with the default parameters, the yellow bands are the Fractional Bands, with the same default parameters (without α, which we don't need anymore since we are not using equation (2)):



We can also compare the Fractional Bands (in yellow) with the Bollinger Bands (in blue-green) , to confirm what we expect from the above equation:



We indeed see that whenever the Fractal Dimension crosses the 1.5 line (i.e. whenever H crosses the 0.5 mark), the respective bands cross as well. The Fractional Bands are therefore narrower for a side-market and wider for a trendy market (even wider than the Fractal Bands for a very trendy market).

The script of Fractional Bands can be downloaded from this address.
The paramaters for the Fractional Bands are the same as for the Fractal Bands except that there is no α, and in addition, we have the following parameter:
PIP_Convertor (integer): the factor necessary to convert real price to PIPS, default is 10000 (for EUR/USD)

As for the strategy, I am not sure whether there is one for this indicator alone, it seems to cross the prices quite often, especially during a side-market, it may however be combined efficiently with the FGDI and/or the Fractal Bands.

From Bollinger to Fractal Bands

Bollinger Bands indicator is a well-known and interesting indicator, as it provides with entry and exit points. It basically consists in a MA and two bands above and below it. Each band is classically placed at 2 standard deviations away from the MA. If we assume that price variations follow a normal distribution, this ensures that 95% of the prices will fall within the bands.
______________________________________________________________________________________________________

I-Some theoretical points

Keeping this assumption for now, the time-series of price variations can be described by a Wiener Brownian Motion of normal distribution N(0,t). It is interesting to see the probability of the prices to be within the bands is equal to the probability of the maximum of the price (that we will name M(t)) to be within them, as shown below:



For more details and the justification of this formula, see my other blog.
We then see:



Such probabilities are calculated for the theoretical value of the standard deviation of the WBM, the Bollinger Bands, however, calculates an empirical value for it using the well known formula:



Given this practical σ and the theoretical one, we can equate the two:



And knowing the theoretical standard deviation for a FBM (see there), we get the practical standard deviation for FBM (of Hurst parameter H):




II-Implementation of Fractal Bands

A straightforward way to implement Fractal Bands seems to just take classical Bollinger Bands and merely increase the width of the bands by raising the standard deviation to the power of 2H. However, if we do that, here is what we get (the MA is the FRASMAv2, the reference period is 30, the blue bands are Bollinger Bands for the same speed) :



I don't find this indicator very useful (not useful at all actually, for me). It seems necessary here to get some perspective about how we wish to improve on the Bollinger Bands. From my point of view, as a day trader, I feel Bollinger Bands too narrow, the prices hit them too often, especially in a trending market, where I would like to get a clear signal only when the trend is over. But, with Bollinger Bands, most of the trend occurs outside the bands, prompting me to close the trade much too early and basically inciting me not to ride the trend.
Applying equation (1) however, we get the counter-productive effect of narrowing the bands when in a trend, because, in our case of price variation, the standard variation is much lower than 1(this may not be the case for stock exchange, but it clearly is for FOREX), raising it to a higher power therefore decreases its value proportionally.
A way out of this quandary is simply to apply the following treatment to the standard deviation from the Bollinger Bands instead of the one from (1):



By taking α greater than 1, the higher our H, the wider the bands will be, here is what it leads to (with the same setup as before, and α=2):



The script fractal_bands.mq4 can be downloaded from this address from the MQL4 site.
The input parameters of the indicator are as follows:
e_period (integer): This is the period considered for calculating the fractal dimension, default is 30.
normal_speed (integer): This is the speed of the SMA before being modified to become the FRASMA, default is 30.
alpha (real): This is the alpha from equation (2), default is 2.
shift (integer): This is the number of bars the FRASMA is shifted to the right(positive) or to the left(negative), default is 0.
e_type_data (0,1,2 or 3): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW), default is 0.


III-Strategical considerations

I have started using the Fractal Bands indicator, and am very happy of it so far. The strategy is quite straightforward.
I enter in a BUY position after the price have rebounded (after touching it) from the lower band and crossed the FRASMA, my Stop Loss is then set to the level the prices hit the lower band, and my Take Profit is when the prices hit the higher band.
Symmetrically, I enter a SELL position after the price have fallen from the higher band (after touching it) and crossed the FRASMA, Stop Loss set at the level of the hit of the higher band, and Take Profit when the lower band is hit.
It is obviously possible (and even advised) to make your Stop Loss trailing the price changes.
I used this strategy for EUR/USD on a 5 minutes timeframe, using it on other timeframes or on other instruments may require a different setup, mine was to set the speed of the FRASMA at 30, and α=2 (in equation (2) above), it is possible to change these values.

Fraternité

Some interesting remarks about fraternity came to my attention today, and I think it reveals an interesting difference between a social policy and Socialism, a confusion that many seem to make, in one sense or another.
First, here is a quote from Charles Péguy's "De Jean Coste" written in 1902 (first the original in french, followed by my translation):

Le devoir d'arracher les misérables à la misère et le devoir de répartir également les biens ne sont pas du même ordre : le premier est un devoir d'urgence ; le deuxième est un devoir de convenance ; non seulement les trois termes de la devise républicaine, liberté, égalité, fraternité, ne sont pas sur le même plan, mais les deux derniers eux-mêmes, qui sont plus rapprochés entre eux qu'ils ne sont tous deux proches du premier, présentent plusieurs différences notables ; par la fraternité nous sommes tenus d'arracher à la misère nos frères les hommes ; c'est un devoir préalable ; au contraire le devoir d'égalité est un devoir beaucoup moins pressant ; autant il est passionnant, inquiétant de savoir qu'il y a encore des hommes dans la misère, autant il m'est égal de savoir si, hors de la misère, les hommes ont des morceaux plus ou moins grands de fortune ; je ne puis parvenir à me passionner pour la question célèbre de savoir à qui reviendra, dans la cité future, les bouteilles de champagne, les chevaux rares, les châteaux de la vallée de la Loire ; j'espère qu'on s'arrangera toujours ; pourvu qu'il y ait vraiment une cité, c'est-à-dire pourvu qu'il n'y ait aucun homme qui soit banni de la cité, tenu en exil dans la misère économique, tenu dans l'exil économique, peu m'importe que tel ou tel ait telle ou telle situation ; de bien autres problèmes solliciteront sans doute l'attention des citoyens ; au contraire il suffit qu'un seul homme soit tenu sciemment, ou, ce qui revient au même, sciemment laissé dans la misère pour que le pacte civique tout entier soit nul ; aussi longtemps qu'il y a un homme dehors, la porte qui lui est fermée au nez ferme une cité d'injustice et de haine.
De Jean Coste, Charles Péguy, éd. Acte Sud Labor L'Aire, coll. Babel, 1993, p. 55

The duty to lift the destitute off their misery and the duty to distribute wealth equally are not of the same order: The former is a pressing duty; the latter is a desirable one; not only the three terms of the republican motto, liberty, equality, fraternity, are not at the same level, but the last two themselves, have several important differences; by fraternity we are prompted to lift our brothers the men off misery; it’s a prior duty; on the contrary the duty of equality is much less pressing; as much as I am passionately disturbed to know that there are still men in misery, as much as I am indifferent to know if, out of misery, men have larger or lesser wealth; I cannot succeed to make myself passionate for the famous matter of knowing who will get in the future society, the bottles of champagne, the rare horses, the castles of the Loire Valley; I hope we’ll always find some arrangement; provided there really is a society, that is, with the provision that nobody will be banned from it, kept in exile in economic misery, kept in an economic exile, nevermind that this or that one is in this or that situation; many other problems will request the attention of citizens; on the contrary, it is enough that one man is kept knowingly, or, which is the same, is knowingly left into misery for the whole social contract to be broken; as long as there is one man outside, the door that is shut in someone’s face secures a society of injustice and hatred.

I think it illustrates very well an aspect of our societies on which we can ponder with some profit. Fraternity is really at the core of humanity and humanism, and its difference with equality is precisely parallel to the one between a social policy and Socialism.

For the french speakers (and listeners), it is also interesting to listen to today's broadcast of Repliques on France Culture:
Repliques du 2 Mai 2009: Penser la fraternité

FRASMAv2

This is an updated version of the FRASMA, earlier discussed. The original logic of it is left untouched, I merely updated it to take into account the calculation of the fractal dimension after the corrections I made in FGDI. Also, following a request from a reader, I added a parameter "shift" who simply translates the FRASMA either to the right (when "shift" is a positive integer) or to the left (when "shift" is a negative integer).

Here is how the FRASMAv2 with a shift set to 10 looks like:



The script for metatrader of FRASMAv2 can be found here.

From D.H. Lawrence to Messiaen

Let me start this post by a quote from Lawrence's "Aaron's rod", towards the end of the chapter "Florence", wherein the hero Aaron plays a piece of solo flute for the Marchesa, who used to be a dilettante singer (contralto), but is now (after WW1) in a sort of downbeat mood, and feels nausea when listening to music (especially the orchestral one):

...And there, in the darkness of the big room, he put his flute to his lips, and began to play. It was a clear, sharp, lilted run-and-fall of notes, not a tune in any sense of the word, and yet a melody, a bright, quick sound of pure animation, a bright, quick, animate noise, running and pausing. It was like a bird's singing, in that it had no human emotion or passion or intention or meaning--a ripple and poise of animate sound. But it was unlike a bird's singing, in that the notes followed clear and single one after the other, in their subtle gallop. A nightingale is rather like that--a wild sound. To read all the human pathos into nightingales' singing is nonsense. A wild, savage, non-human lurch and squander of sound, beautiful, but entirely unaesthetic.

What Aaron was playing was not of his own invention. It was a bit of mediaeval phrasing written for the pipe and the viol. It made the piano seem a ponderous, nerve-wracking steam-roller of noise, and the violin, as we know it, a hateful wire-drawn nerve-torturer.

After a little while, when he entered the smaller room again, the Marchesa looked full into his face.

"Good!" she said. "Good!"

And a gleam almost of happiness seemed to light her up. She seemed like one who had been kept in a horrible enchanted castle--for years and years. Oh, a horrible enchanted castle, with wet walls of emotions and ponderous chains of feelings and a ghastly atmosphere of must-be.
She felt she had seen through the opening door a crack of sunshine, and thin, pure, light outside air, outside, beyond this dank and beastly dungeon of feelings and moral necessity. Ugh!--she shuddered convulsively at what had been. She looked at her little husband.
Chains of necessity all round him: a little jailor. Yet she was fond of him. If only he would throw away the castle keys. He was a little gnome. What did he clutch the castle-keys so tight for?

Aaron looked at her. He knew that they understood one another, he and she. Without any moral necessity or any other necessity. Outside--they had got outside the castle of so-called human life. Outside the horrible, stinking human castle Of life. A bit of true, limpid freedom. Just a glimpse.

It is always difficult to discuss such a passage without, somehow, destroying its charm. I will therefore limit myself to providing a few directions through which its understanding may be deepened (or so it is for me).

First, I'd like to qualify a little the rather harsh judgment about the piano, by referring to composers such as Satie (one may also relate the mediaeval flavour of what Aaron plays to Satie's world) or Mompou, who found a voice for it that does not deserve to be called ponderous or nerve-wracking, and Messiaen, who seemed to echo the comparison of Lawrence with birdsongs, by composing his "Catalogue d'oiseaux", and that one was mostly composed for piano, even though, the first piece of this collection can be said to be "Le merle noir", itself composed primarily for the flute (with a piano accompanying).

On the other hand, the piano indeed has a tendency towards grandiloquence, from which the flute seems immune. One may think of Japanese music, and of the often central part played by the shakuhachi (wooden flute), and that may be the best approach to enter the "out-of-life" world (though I disagree with this characterization) Lawrence is talking about in this passage. The wonderful recording by Lily Laskine and Jean-Pierre Rampal came readily to my mind while reading these lines.

But before the "Catalogue d'oiseaux", even before "Le merle noir", there was Messiaen's "Preludes pour piano", whose first piece is called "La Colombe", already a bird, even if this one is a metaphor for Messiaen's mother. This piece, at least for me, particularly resonates with Lawrence's point.

Fractal dimensions...And a Fractal Graph Dimension Indicator

I have already alluded to the possible confusion with regard to what the fractal dimension exactly is, and even though I try to always clarify the kind of fractal dimension I am considering in a given context, I never provided with a detailed discussion of this problem. So here it is, I am going, in this overview, to discuss the various definition of this entity, and give some references which examine their relationship in more detail.
Eventually, I shall provide with a new indicator that slightly improves on the previous calculation of the fractal dimension of a graph.

1) Hausdorff Dimension (or Besicovitch-Hausdorff Dimension).
This is the oldest and most mathematically convenient definition of the fractal dimension of an object, but it is also extremely difficult to calculate exactly for most object, especially those who are not exactly self-similar, which is basically the case of all interesting objects in any applied domain.
We first need to define a measure of an object F as such:



Where a δ-cover is a countable (or finite) collection of sets of diameter at most δ that covers F.
The s-dimensional Hausdorff measure of F is then defined as:



The Hausdorff Dimension is then defined as:



The difficulty in computing this quantity lies in the definition of a δ-cover. The sets of the collection are indeed not necessarily having a diameter of δ, on the contrary, it will be frequent to have an optimal collection (in the sense of optimizing equation (1)) that will have sets with a diameter much smaller than δ, and to explicit the logic behind such a construction is only possible for extremely simple sets (typically, sets that are explicitly built through a well-known iterative process). That is obviously not the case of sets found in practice as a model of a real phenomenon.
This difficulty can be overcome by the Box-counting Dimension to which I come now. For more details about the Hausdorff Dimension see Chapter 2 in [FALC03].

2) Box-counting Dimension (or Kolmogorov Entropy, Entropy Dimension, Capacity Dimension, Metric Dimension, Logarithmic Density and Information Dimension)
The Box-counting Dimension can be defined simply as:



Where can be any of the following (not exhaustive list):
- The smallest number of closed balls of radius δ that cover F;
- The smallest number of cubes of side δ that cover F;
- The number of δ-mesh cubes that intersect F;
- The smallest number of sets of diameter at most δ that cover F;
- The largest number of disjoint balls of radius δ with centres in F.

From the definition of both the Hausdorff and the Box-counting Dimension, it is easy to see intuitively (from equation (1)) that:



For a formal proof of that and more detail about the Box-counting Dimension, see Chapter 3 in [FALC03].
There are some other alternatives to define the fractal dimension, but so far, I have not seen applications of those to finance, and therefore, I will not mention them here, see [FALC03] for a short overview of those.

3) Fractal Graph Dimension Indicator
I have already referred to the code written by iliko that implemented a calculation of the fractal dimension. This computation is actually inspired from this article that provides with a method to estimate the Box-counting Dimension (and not directly the Hausdorff Dimension as it is claimed in the article itself)(see equation (6) in the article).
I however noticed two slight mistakes in iliko's code:

- At line 199:
Instead of : for( iteration=0; iteration < g_period_minus_1; iteration++ )
It should be : for( iteration=0; iteration <= g_period_minus_1; iteration++ )

- At line 213:
Instead of : fdi=1.0 +(MathLog( length)+ LOG_2 )/MathLog( 2 * e_period );
It should be : fdi=1.0 +(MathLog( length)+ LOG_2 )/MathLog( 2 * g_period_minus_1)

After correction however, there is not much change in the indicator itself.
In addition I added a calculation of the standard deviation of the fractal dimension so estimated. It is also given in the article as equations (10) and (11); and that may provide information for a more precise entry point for a trade.
The MQ4 file of the FGDI Indicator can be downloaded from this address in the MQL4 Community forum.

Here is a daily EUR/USD chart representing this new indicator along with the FRASMA, and the original fractal dimension by iliko (lower window):

A trading strategy using the Fractal dimension

On this forum, somebody is proposing an Expert Advisor for MT4, with an automated strategy to enter the market that uses the Fractal Dimension.

I believe some improvements can be made, and I have shared my thoughts on the thread itself, and will continue to do so as it develops.

Canon cancrizans

Here is a mathematical illustration of the "canon cancrizans" from J. S. Bach’s “Musical Offering” (1747), that will refresh the memory of Douglas Hofstadter's "Gödel, Escher, Bach: an Eternal Golden Braid" readers:
Canon 1 a 2

FX Scaling Laws

This article by Glattfelder, Dupuis and Olsen, brought to my attention by a reader, proposes an empirical set of scaling laws that apply to FX markets.
After considering them, in view of devising an interesting indicator for trading, the problem appears to be that these laws mostly concerns averages taken over 5 years, that is a serious limitation for their applicability on a short period of time.
Nonetheless, I identified one, the law (12) that may be of interest, provided some more work:



This law(applied to the total move, *=tm) gives the length of the coastline for a given pair for a year of activity (250 days) as a percentage, relatively to a resolution defined as the directional-change threshold (cf chapter 2.3 in the article).
Considering the case without the transaction costs (an assumption, I think, justified by the small scale considered), I then look at Table A19 to know the parameters of the Law relative to the currency pair I am interested in. For the following I will consider EUR/USD, which is the pair I trade most often, the law therefore becomes :



As I am interested in moves around 10 PIPs, I shall then consider a resolution of 0.001 for EUR/USD, so:



Which gives me a resolution between 12 and 14 PIPs (for the current value of the EUR/USD) since 0.001 is a percentage.
As a result, I get:



This is the annualised length of the coastline, I am more interested in this length for 15 minutes, I therefore have to divide it by 250*24*4, for a result of:



Which is equal to about 520 PIPs (taking 1.35 for EUR/USD) as the length of the coastline for 15 minutes.

This information is the best I can get so far from the scaling laws described in the article. It may be used to determine the width of a channel (volatility), though, even for this, it needs to be included in further calculations (that will likely used the Graph Dimension, or the Hurst exponent). I am currently thinking of ways to do that, and will publish any success I may have with this line of thought in the future.

Is bargaining anti-capitalistic ?

Let me indulge a bit more in some economic ranting while I am still on holiday.

It is easy to verify the fact that bargaining is most popular in those places the less developed in terms of capitalism, and the more a country will "progress" in accepting the principles of modern capitalism, the more the activity of bargaining will disappear. It may almost seem like paradox, but is it really one?
I come to think of a possible explanation for this phenomenon, whether it accounts totally for it or only partially can certainly be a matter of debate.

Bargaining is properly a confrontation between one offer and one demand, it is a highly individualistic process. Despite that the offerer can back his side of the exchange by a direct reference to the overall demand for the specific product, and on this ground he will argue for a higher price than the customer is ready to pay. On the other hand, the customer can argue that this overall demand is merely virtual, projected, but ultimately unrealized in the very short term, while his present buying of the goods means immediate, actual money for the seller.

That's how it used to be in traditional societies, in those areas where the exchange of goods was falling beyond the reach of the despotic rulers. It seems odd then to think that an extension of the domain of free exchange(Capitalism) has entailed a quasi disparition of bargaining.
Bargaining assumes that the price of a commodity is open to debate, it is not a static given of the transaction, on the contrary, it is a dynamic component of it. Opposite to this, obviously lies the principle that any given commodity has a fair ("natural") price. If nowadays, a customer intend to bargain, the selling person(who is likely to work for a salary, not even indexed on his selling performance) can simply reply, that the price displayed is already the optimal price, and that there is nothing better to hope for.

One may then say that the almost disappearance of bargaining is simply an effect of the mass-consumption and the bureaucratization of the modern world, and that it has nothing to do with Capitalism, I believe Schumpeter[1] may disagree with that with regard to the origins of modern bureaucracy, that he saw as a manifestation of the rationalization of the economic and social life (the latter being largely conditioned by the former in a capitalist system).
So, even if bargaining could have survived the rational theory of commodities exchange that has developed after Ricardo, and evolved into the neo-classical theory, and its widespread acceptation by our societies, it seems difficult to imagine that it could have survived its multifarious pervasive effects.

I would therefore say that bargaining is NOT anticapitalistic, I believe it is on the contrary, the most genuinely capitalistic activity one can think of: It is the epitome of individual freedom at the level of the most elementary economic transaction, the freedom of agreeing on a price.
Clearly this freedom is not denied in the direct sense of fixing the prices of goods by laws as what may be thought of in marxist-inspired societies, but an indirect influence is just as powerful and much more difficult to identify. Prices are also fixed in modern Capitalism, by sophisticated economic theories about which Georgy Lukacs once said that a statue should be erected for their authors in front of every ministry of economy in the communist countries, because they are the main contributors to the practice of state socialism (I think it is Lukacs, but if someone wants to correct me and can cite the exact quote, I will be happy to correct this post in the sense necessary).

What bargaining is clearly incompatible with, is the ideology that affirms the existence of an objective natural price, in a sense not far from the existence of a natural law. It is that ideology that takes away from the individual negotiation the freedom of fixing the price for an individual transaction.

On a side-note, the sociological dimension of bargaining could also be an interesting topic of discussion. I mean by that the way such an activity exceeds the merely utilitarian aspect of commodity exchanges and may be a strong basis for building or consolidating a network of social human relationships, with diplomacy and common understanding as a basis. Maybe somebody can point me towards some authors who investigate these aspects.

References:
[1]: Capitalism, Socialism and Democracy

For a deontological code in Finance

I came through the following article[1], that provides with an analysis of the responsibility of Finance and Economics Academia with regard to the current crisis, and one of their conclusion is as follows:

A second, more likely explanation, is that they did not consider it their job to warn the public. If that is the cause of their failure, we believe that it involves a misunderstanding of the role of the economist, and involves an ethical breakdown. In our view, economists, as with all scientists, have an ethical responsibility to communicate the limitations of their models and the potential misuses of their research. Currently, there is no ethical code for professional economic scientists. There should be one.

I certainly agree with that, but for such warnings about the models to be heard in the capitalist world we are living in, they must be broadcasted quite loudly, and even enforced by some sort of regulations. Some people just don't want to hear certain truths, especially when these ones are liable to jeopardize their multi-millions bonuses. Let's keep in mind that most financial researchers are funded by these people (directly or indirectly), and that they therefore are cordially invited to present results that are pleasing to their benevolence.
If speculators pay for the financial researches done in academia, is it such a big surprise to find that these researches tend to show the harmlessness of speculation?

While the overall article is interesting, I'd like to comment a bit on the following:

Of course, considerable progress has been made by moving to more refined models with, e.g., ‘fat-tailed’ Levy processes as their driving factors. However, while such models better capture the intrinsic volatility of markets, their improved performance, taken at face value, might again contribute to enhancing the control illusion of the naïve user.

The user who thinks that Levy processes may somehow enhance his control, is not naïve, he is ignorant of what a Levy process is all about. Levy process is exactly telling us that we have less control about what's going on, and particularly, it invalidates the dynamic hedging strategy inspired by Black, Merton and Scholes work. Furthermore, this invalidation is not a matter of opinion, it is a matter of mathematical correctness, as Haug and Taleb have shown in the previously cited article (Haug and Taleb, November 2007), a Levy distribution entails such a weakening of the Central Limit Theorem that the hypothesis(finite variance) making possible dynamic hedging becomes false.

And last but not least, it would be unfair not to mention the existence of the Truncated Levy Process(TLF) that seemingly resolved the "inconvenience" of the Levy Process with regard to the infinite variance, and therefore bring it back to the scope of validity of the Central Limit Theorem, making Dynamic Hedging again possible. It is indeed what Andrew Matacz in this article[2] aims at achieving.
While I don't question the value of the mathematical parts in the article, I wonder about their applicability from an investment point of view, and there's indeed a profound ethical problem at play here, and it is rooted in the belief of the possibility of a riskless strategy (which is at the core of Dynamic Hedging). There can't be such a strategy, because if there was one, its implementation would invalidate it (the statistical model of a market is always historical, the market can perfectly shift from one model to another, it is not causally determined to stay within the limits of one precise model).
A riskless strategy is potentially the equivalent of the perpetual motion machine in mechanics, to use it may well lead to its destruction (and also create a speculative bubble in the process).
On the other hand, the study of TLF is interesting and should be pursued, but it is necessary to separate this study from the sole motivation of creating an investing edge in the market (again the problem of deontology and financing creeps back). In this sense, the approach of Cont, Potters and Bouchaud in this article[3] from May 1997, displaying as its primary concern the fitting with existing data, appears more promising.

References:
[1]: The Financial Crisis and the Systemic Failure of Academic Economics
[2]: Financial Modeling and Option Theory with the Truncated Levy Process
[3]: Scaling in stockmarket data: Stable laws and beyond

An ongoing discussion

In relation to my last post, about the "flapping butterflies", a discussion is going on between myself and Duc on his site, it takes place over several posts, so a bit difficult to follow, but in case some of my readers are interested.

Also, I updated the format of comments here, so that, anybody can now post one, even as anonymous if one wishes. I actually did not realize earlier that there was some limitations on this.

Flapping butterflies don't make hurricanes (A critical view of the 2008-2009 crisis)

Many analysts have provided, are providing, and will provide still for some time with explanations of the current crisis, and often conclude by sketching some remedies to it, or at least which system should be implemented in the future to avert a similar situation. I seldom totally disagree with those explanations, but I even more rarely totally agree with them, and I almost never share their sketches of a solution.
Ultimately though, I think the core problem is seldom touched at all.

As for the elements commonly incriminated for the crisis, here are a few in no order:
- CDS and their unregulated practice
- SubPrime loans and their securitization
- Expansionary monetary policy of the central banks (primarily the one from USA)
- Intervention of the US government to promote access to home ownership (primarily the Community Reinvestment Act)
- The carelessness of the Credit Ratings Agencies
- The dogmatic culture in financial mathematics (relying on a Gaussian model) that promoted risky strategy by presenting them as riskless
- American over-consumerism and over-reliance on credit
...etc.

According to the analyst, some of these phenomena will be emphasized, others may simply be ignored or neglected, but each will be weighted in order to rationalize a judgment that often appears to have preexisted to a fair analysis, and the rhetorics betrays more or less clearly a whole set of prejudices that is not very difficult to relate to a school of economics.
It is clear to me that all these elements (and many others) have played a role at one time or another in the unfolding of the crisis, it is however very difficult and hazardous to identify their relative importance.

Rather than contributing to this debate by merely adding my own prejudices and rationalization, I will try here to bring up a few elements that I have not seen often mentioned (if at all).

1)I saw many who tried to put the key responsibility of the crisis on government intervention, some defending the point that in absence of such intervention, crisis would simply not develop at all, at least not up to any significant level. This idea is simply false and has been demonstrated to be so in 1966 by Mandelbrot in an article[1], reprinted as the chapter E19 in [MAN97]. In the reprint, Mandelbrot includes the following foreword:

Two terms are found in the title of this reprint, but not of the originals, namely "nonlinear" and "rational bubble". They express the two main points of this paper in words that were not available to me in 1966.
The main substantive finding was that rational behavior on the part of the market may lead to "wild" speculative bubble(...). The randomness of these bubble is called "wild" in my present vocabulary, because they can be extremely large, and their sizes and duration follow a scaling distribution. This distribution is closely akin to the L-stable distribution introduced in the model of price variation presented in M 1963b.

In there, Mandelbrot demonstrates how speculative bubbles do occur "naturally" in a market. While it is very possible that some interventions will facilitate bubbles, this mere possibility allows for the opposite one, that some intervention can also diminish the intensity of bubbles, and even prevent their apparition or their violent burst.
The prejudice that roots speculative bubbles in government intervention (read as disturbances of a market otherwise well-balanced) is untenable.

2)One reading of this crisis can be that of the failure of dynamic hedging. I can't testify about the importance of this failure and its relevance in this crisis, but if I am to believe Espen Gaarder Haug and Nassim Nicholas Taleb in this article[2], and if dynamic hedging was used in any systematic way by the main financial institutions, there is certainly some kind of responsibility to be found here.
At the root of the popularity of dynamic hedging, there is again the dogma that markets are inherently Gaussian, and eventually do not derive into fat-tailed behavior (where serious bubbles form and burst). This is obviously a denial of the reality of their nature, a nature that has been largely documented over the last 40 years, and clearly displays a chaotic behavior.

3)Another type of analysts, while recognizing the correctness of the occurrence of crisis in an unhampered market, will argue that any intervention can only make things worse, human minds simply cannot understand the full effect of their actions, and in a complex system such as the economy, they better abstain from any attempt to act.
I can't help seeing the fundamentally religious mindset behind such a position, in that it hypostasizes the market into an order beyond human understanding, that seems to exist in a transcendental realm: From a mere metaphor, the "invisible hand" suddenly becomes the Logos, the infallible organizing principle.
This rationale though, hinges on a misunderstanding of the "Butterfly Effect". This famous effect is known by most, and for most, it is the only thing they know about Chaos Theory (and Fractals), and the dynamics of complex systems, but no butterfly ever created a hurricane, the image is simply that, again, a metaphor to say that very slight disturbance may contribute to(rather than create) unforeseen catastrophic effect. It does not mean that they always do so, or even that human understanding cannot have any control over the most adverse of these effects. Real complex systems have some level of tolerance, of self-regulation at a local level, of resilience (to use a fashionable term). We may not control the weather, but we can open an umbrella not to get wet when it rains, and it does not make the rain any heavier.
Human beings are acting, whether in relation to the weather or in relation to the market, there is no such thing as an unhampered market, because there is no such a thing as a market without human actions.
The question is whether we should think those interventions in a rational manner, from a social point of view, or whether we should leave each individuals to impose themselves in the market on the basis of their luck, intelligence and birth, and let the big picture to the care of the "invisible hand" (if one has faith in its omnipotence, with regard to this context, this faith anyway falls beyond rationality).

In conclusion, let me expose my opinion, which may be prejudiced, but if so, I welcome any criticism of it.
I see the root of the current crisis in this core belief, of a religious nature, about the market (as self-regulated by the "invisible hand"), that led many people to ignore what the market really was, because it was inconvenient for them to acknowledge it (its chaotic nature was going against the belief).
The origin of this credo can be found in the Cold War (which provided a propitious intellectual climate for such a faith to flourish: Against the religious socialism of the communist block, a religious form of capitalism was seen as most welcome), and more precisely in the Neo-conservative ideology that succeeded to fusion several elements of economic thought mostly coming from the Austrian school, Monetarism and Libertarianism; it further blended these elements with the US christian movements that spread from (or were heavily influenced by) Calvinism, Pietism, Methodism and Baptism (cf. Max Weber[3] about the historical link between protestant sects and Capitalism).
As a result, a very dogmatic and religious ideology came into play as the official economic philosophy of american politics (beyond traditional party lines) and even found strong supporters in western Europe (until recently, Sarkozy and Berlusconi were among them). It found its natural expression in a minimization and constant undermining of political power (and of the legitimacy of democracy, and therefore of democratic intervention), to the profit of economic institutions (not submitted to the control of the public in any way) and capitalist actors, the latter often providing the very people in control of the former, a kind of crony "democracy" and neocorporatism (very much acquainted with its fascistic counterpart) developed on this basis. This phenomenon is well documented, as early as the late 80s by Habermas in Ecrits Politiques[4] (sorry, I don't know the english version or even whether there is one).
It is eventually this ideology that I will rank as holding the primary responsibility for the current situation; and one may still see its influence at work in the ways the crisis is analysed, and recommendations are made to decrease even more the influence of the government in the economic realm.

References:
[1]: Forecasts of Future Prices, Unbiased Markets, and "Martingale" Models
[2]: Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula
[3]: The Protestant Ethic and the Spirit of Capitalism
[4]: Ecrits politiques

The speed of the FRAMA (Part 2): The FRASMA

Having explained my preference for a "fractalisation" of the MA to apply on a SMA(rather than on an EMA), I shall now discuss the exact form of this "fractalisation".
A modification, close to the one recommended by Ehlers, would be to merely divide the period of the SMA by the coefficient α, where α is defined as:



For a dimension D varying between 1 and 2, such a division would indeed be equivalent to a change of speed in a ratio of 100, the SMA being slowed down 100 times from its initial pace, in the extreme case of a dimension of 2.
This dimension D is a numerical approximation of the Box Dimension, itself an approximation of the Hausdorff dimension of the graph, which is properly the most mathematically precise fractal dimension. There is however, another dimension that can also be seen as a Box Dimension, but of another object relating to the process under study, and that Mandelbrot called the Trail Dimension [MAN97,pp.161&172).

For a Fractional Brownian Motion, we saw earlier that:



Where is what we have called so far the Fractal dimension, and α is the coefficient of the FBM (which is a different thing from the α of equation (E1)) . This latter is actually known as the Hurst-Holder exponent (or sometimes as simply the Hurst exponent, in memory of the British hydrologist whose studies of the long-term dependence of the Nile discharges, were inspirational to Mandelbrot works), and most often designed by H, I used α in reference to Falconer's book, but H seems more convenient from now on. We therefore have:



And will now be known as the Graph Dimension. While the Trail Dimension will be defined as:


_________________________________________________________________________________________________________________

I-Interpretation of the Trail Dimension

It is easy to see that the Trail Dimension varies between 1 and ∞, for the coefficient H varying between 1 and 0. The first question is therefore how a "dimension" growing infinitely should be understood. In [MAN97], p.161, Mandelbrot wrote the following explanation:

"First consider a Wiener Brownian motion in the plane. Its coordinates X(t) and Y(t) are independent Brownian motions. Therefore, if a 1-dimensional Brownian motion X(t) is combined with another independent 1-dimensional Brownian motion Y(t), the process X(t) becomes "embedded" into a 2-dimensional Brownian motion {X(t),Y(t)}. The value of the trail dimension:

is the fractal dimension of the three dimensional graph of coordinates t,X(t) and Y(t), and the projected "trail" of coordinates X(t) and Y(t). However, the dimension:

applies to the projected graphs of coordinates t and X(t) or t and Y(t)."

My understanding of the above passage, in the general case of FBM (H varying between 0 and 1, while for WBM, H=1/2), is that the Trail dimension must be seen as an approximation of the number of dimensions in which the "real" process takes place (here it might be interesting to understand the term of "dimension" in a data-mining sense, rather than in a strict topological sense, prices are clearly the end-result of many independent processes, any of them with the potential of being chaotic in their own right), under the assumption that all the coordinates of the said process can be described as independent Fractional Brownian motions sharing the same Hurst exponent.

II-Slowing down the MA with the Trail Dimension

It is now possible to conceive of a formula for the coefficient α, using the Trail Dimension. The purpose of α is to slow down the MA from a reference speed when the Hurst exponent becomes very small, and also to accelerate it when this exponent becomes close to 1. The reference speed should be taken as the one used when the price varies in a gaussian way, that is when H is 1/2. So for such a value of H, we should have α=1.
If we then consider the following formula:



For a WBM, we have α=1. In addition, for a H tending towards 0, α tends towards infinity, and for H close to 1, α=1/2.
Comparing α from (E2)(red curve) with the inverse of α from (E1)(black curve)(we take the inverse in order to get a multiplicative factor rather than a dividing one to apply on the speed of the MA), we get the following graphs:



Or, for a more detailed view of their behavior below H=1/2:



Dividing the black curve by 10 in order to have an unchanged speed for the case of a WBM, we get the following:



For H varying from 0.5 to 0, we see that the α coming from (E1) varies almost linearly, for the same variation however, we know that the randomness increases in a rather non-linear fashion; a linear slowing down of the MA does not seem to reflect this properly. From this theoretical point of view, I therefore prefer the α given by equation (E2)(not to mention that it is much more simple).

III-Implementation of the FRASMA

I programmed the FRASMA(Fractally modified Simple Moving Average) in the MetaTrader platform. You may access and download freely this indicator, as well as use it on the metatrader 4 platform, at this address of the MQL4 Community.
Please, let me know your findings or any criticisms that can improve this indicator.
Meanwhile, here is a screenshot of three fractally modified MA, the Light Blue is a version of the FRAMA from Ehlers paper (modifying a EMA), the Yellow is a modification of a SMA using the following α inspired by Ehlers paper:

And the Red one is properly the FRASMA, using equation (E2).



Below is the fractal Graph Dimension. The period of reference for all original MA is 20.

IV-Conclusion

My purpose here is not to demonstrate that one indicator is better than another, since the quality of an indicator is relative to the manner one uses it. I believe that one must be acquainted intuitively with an indicator to use it productively, and it is for this reason that my preference is going to the FRASMA.
While one may just rely on direct practise to "understand" at an intuitive level a given indicator, I believe most of us can also profit from a theoretical understanding of them. My goal here is therefore to provide elements along these lines, for others to develop their own familiarity, and maybe provide me, in return, with some of their insights and experiences.
It is again naive to think that a trader, using technical analysis, can actually trade without some level of reliance on his intuition, and it is to totally miss the point of what the fractals tell us about the market to nourish expectations about a deterministic methodology to be successful as a trader, in other words, there is no Grail to be found in the first place. Nonetheless, to understand the technical tools one is using, can improve one's intuition, and the overall success of one's trading activity.

Tuning up the mind

In The Nature of Risk, Justin Mamis concludes his sixth chapter with the following remark:

Intuition, although seemingly spontaneous, apparently emotional, stems from a form of "information" that has become built-in from past experience. Discipline means choosing what to do unencumbered by the fear of making a mistake. Confidence means trusting our intuition that what we "see" is what we "know." There's no escaping to the external, to the objective, and no standing on the shaky ground of emotions. So the question becomes, How do we create within ourselves the heroic condition of confidence wherein risk is not danger but life.[MAM99, p.80]

The condition of confidence, heroic or not, to be actual, must somehow not deceive too much, and it would be naive to think that intuition never deceives us. Nonetheless, Mamis is right, intuition is a critical component in any decision process, not less in a trading context.
Technical analysis is very nice, but if fractal geometry teaches us anything, it is that we cannot foresee the evolution of complex processes on the basis of objective knowledge.
Now, if intuition deceives us, I contend that it is because it is trained to do so: Our whole education has conditioned us to think in deterministic terms, the analytical mind is praised and rewarded, hard sciences have simply excluded complex systems from their scope for centuries, and these systems are hardly touched at all in a normal education before a specialized Masters level even today.
Despite that, hard sciences and the mode of thinking they promote, are the foremost influence we are exposed to during our formal education. We are all members of the church of scientism, those who are not are likely to be members of churches even more deterministic than this one.
And our intuition follows this fold, even when we lack information to make a decision (which is almost always the case), we will tend to over-rely on the ones we have, and decide solely on this basis, extrapolating linearly from this partial knowledge, because we are conditioned to rely on linearity. We are simply unable to recognize, acknowledge and take into account the non-linearity of a process. It is this ability that must be developed over time, and it is this one that shall be called an efficient intuition.

There is one domain of the culture that may provide us with a way to build up this intuition, and that is Art. To each his own, personally, I am more sensitive to music and poetry, and it is therefore along these lines that I will argue my point, but I believe it can be transposed to other arts.
Adorno's critic of Schoenberg's and Stravinky's music links them both to the political and philosophical problematic of their times:
Art, indeed, always happens in a context, and relates to it in a very essential way, furthermore, it always takes on a problematic and resolve it figuratively. When Bartok or Stravinsky rejuvenated classical music with peasants songs, they merely reacted to the standardization of the world along western romanticist lines. But more than that, they provide us with a solution to the problematic of cosmopolitism, the native cultures don't have to be erased, they can be consolidated within an evolving culture (civilizations don't clash, they merge, sorry Mr.Huntington) and contribute to a manifold society (see the cosmopolitanist philosophy of Kwame Anthony Appiah for instance). The european empires could have used a bit of insight from them in the 20s and 30s.

And the same goes for today, here is a piece by Iannis Xenakis: Metastasis
The 1st and 3rd movement deals with a relativistic notion of time, that is a function of energy and mass. Interestingly, in trading, Mandelbrot defines the concept of trading time, which is also a function of what can be compared to energy and mass, and that is volume. That is actually a reflection of the dependence of the Hurst-Holder exponent to time [MAN97, pp39-40].
The second movement is even more interesting since it gives a musical translation of Fibonacci sequence.

Xenakis also wrote pieces dealing with Brownian Motion, Normal Distribution and Statistical Mechanics, all very interesting pieces. What they provide us with is an acquaintance that goes beyond the mere knowledge of well-defined criteria, an intuition that may articulate our decisions in a more efficient way.

The speed of the FRAMA (Part 1)

Earlier, I mentioned the logic behind the FRAMA (Fractal Adaptive Moving Average), and merely referred to John Ehlers'article. Here I wish to examine and discuss a bit more in detail this logic.

John Ehlers recommends to link the speed of an exponential moving average to the fractal dimension by making the coefficient α a function of this one via the following formula:



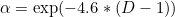
Let's accept this formula, in a first time, to consider the problematic of whether to apply this modification on an exponential moving average(EMA) or on a simple moving average(SMA).

The purpose of the EMA is to give more weight to the most recent price variations, this is a fair concern for the medium or long-term trader, I feel it is however a much less interesting feature for the intraday trader, who has to cope with a lot of noisy, meaningless fluctuations, and relies on the moving average precisely to avoid being distracted by this noise.
Besides, if we look at what happens for a high fractal dimension (approaching 2), the coefficient α is going to be very small (around 0.01, see the FRAMA article referenced earlier), the EMA will then be slowed down, but then, we also know that such a high fractal dimension coincides with the wildest noise, and therefore very high variations of prices. What is then the point of, on one hand slowing down the EMA, while this one will put a higher weight on the most recent, wildest price variations, thereby reflecting the wildness?

The two ideas clearly seem to conflict, and the resulting signal appears to be an ambiguous compromise where the exponential endeavors to speed up the moving average (by emphasizing the most recent variations) while the fractal dimension endeavors to slow it down.

I therefore prefer, especially as an intraday trader, to fractalise directly a SMA, and therefore get a direct and readable translation of the information implicit in the fractal dimension. This can be easily achieved by simply dividing the period of the SMA by the coefficient α.

Complement following a remark by Cool here:

In reply to Cool remark, here is a graph representing the FRAMA from Elhers in yellow, and this same FRAMA using a more precise calculation of the Fractal Dimension in red. Both FRAMA are exponential MA with a reference period of 10, their only difference is in the way the fractal dimension and therefore the coefficient α is calculated:

Yellow curve:
The fractal dimension is computed from the following equation:

where N1=(HighestPrice – LowestPrice) over the interval from 0 to T, divided by T, N2=(HighestPrice – LowestPrice) over the interval from T to 2T, divided by T and N3= (HighestPrice – LowestPrice) over the entire interval from 0 to 2T, divided by 2T
and


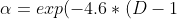Red Curve:
The fractal Dimension is computed from the following equation:




Here are the two MT4 listings.

For the original Elhers FRAMA (Yellow Curve):
//+------------------------------------------------------------------+
//| FRAMA.mq4 |
//| Rosh |
//| http://www.alpari-idc.ru/ru/experts/articles/ |
//+------------------------------------------------------------------+
#property copyright "Rosh"
#property link "http://www.alpari-idc.ru/ru/experts/articles/"

#property indicator_chart_window
#property indicator_buffers 1
#property indicator_color1 DarkBlue
//---- input parameters
extern int PeriodFRAMA=10;
extern int PriceType=0;
//PRICE_CLOSE 0 Öåíà çàêðûòèÿ
//PRICE_OPEN 1 Öåíà îòêðûòèÿ
//PRICE_HIGH 2 Ìàêñèìàëüíàÿ öåíà
//PRICE_LOW 3 Ìèíèìàëüíàÿ öåíà
//PRICE_MEDIAN 4 Ñðåäíÿÿ öåíà, (high+low)/2
//PRICE_TYPICAL 5 Òèïè÷íàÿ öåíà, (high+low+close)/3
//PRICE_WEIGHTED 6 Âçâåøåííàÿ öåíà çàêðûòèÿ, (high+low+close+close)/4

//---- buffers
double ExtMapBuffer1[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function |
//+------------------------------------------------------------------+
int init()
{
//---- indicators
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,ExtMapBuffer1);
SetIndexEmptyValue(0,0.0);
//----
return(0);
}
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
//----

//----
return(0);
}
//+------------------------------------------------------------------+
//| âîçâðàùàåò öåíó |
//+------------------------------------------------------------------+
double Price(int shift)
{
//----
double res;
//----
switch (PriceType)
{
case PRICE_OPEN: res=Open[shift]; break;
case PRICE_HIGH: res=High[shift]; break;
case PRICE_LOW: res=Low[shift]; break;
case PRICE_MEDIAN: res=(High[shift]+Low[shift])/2.0; break;
case PRICE_TYPICAL: res=(High[shift]+Low[shift]+Close[shift])/3.0; break;
case PRICE_WEIGHTED: res=(High[shift]+Low[shift]+2*Close[shift])/4.0; break;
default: res=Close[shift];break;
}
return(res);
}

//+------------------------------------------------------------------+
//| Custom indicator iteration function |
//+------------------------------------------------------------------+
int start()
{
double Hi1,Lo1,Hi2,Lo2,Hi3,Lo3;
double N1,N2,N3,D;
double ALFA;
int limit;
int counted_bars=IndicatorCounted();
if (counted_bars==0) limit=Bars-2*PeriodFRAMA;
if (counted_bars>0) limit=Bars-counted_bars;
limit--;

//----
for (int i=limit;i>=0;i--)
{
Hi1=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i)];
Lo1=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i)];
Hi2=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i+PeriodFRAMA)];
Lo2=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i+PeriodFRAMA)];
Hi3=High[iHighest(Symbol(),0,MODE_HIGH,2*PeriodFRAMA,i)];
Lo3=Low[iLowest(Symbol(),0,MODE_LOW,2*PeriodFRAMA,i)];
N1=(Hi1-Lo1)/PeriodFRAMA;
N2=(Hi2-Lo2)/PeriodFRAMA;
N3=(Hi3-Lo3)/(2.0*PeriodFRAMA);
D=(MathLog(N1+N2)-MathLog(N3))/MathLog(2.0);
ALFA=MathExp(-4.6*(D-1.0));
ExtMapBuffer1[i]=ALFA*Price(i)+(1-ALFA)*ExtMapBuffer1[i+1];
}
//----
return(0);
}
//+------------------------------------------------------------------+

For the FRAMA modified with a different fractal dimension calculation (Red Curve):

//+------------------------------------------------------------------+
//| FRAMA2.mq4 |
//| Copyright © 2008, MetaQuotes Software Corp. |
//| http://www.metaquotes.net |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2008, MetaQuotes Software Corp."
#property link "http://www.metaquotes.net"

#property indicator_chart_window

#property indicator_color1 Red
#property indicator_width1 2
//************************************************************
// Input parameters
//************************************************************
extern int e_period =10;
extern int normal_speed =10;
extern int e_type_data =PRICE_CLOSE;
//************************************************************
// Constant
//************************************************************
string INDICATOR_NAME="FRAMA2";
string FILENAME ="FRAMA2.mq4";
double LOG_2;
//************************************************************
// Private vars
//************************************************************
double ExtOutputBuffer[];
int g_period_minus_1;
//+-----------------------------------------------------------------------+
//| FUNCTION : init |
//| Initialization function |
//| Check the user input parameters and convert them in appropriate types.|
//+-----------------------------------------------------------------------+
int init()
{
// Check e_period input parameter
if(e_period < 2 )
{
Alert( "[ 10-ERROR " + FILENAME + " ] input parameter \"e_period\" must be >= 1 (" + e_period + ")" );
return( -1 );
}
if(e_type_data < PRICE_CLOSE || e_type_data > PRICE_WEIGHTED )
{
Alert( "[ 20-ERROR " + FILENAME + " ] input parameter \"e_type_data\" unknown (" + e_type_data + ")" );
return( -1 );
}
IndicatorBuffers( 1 );
SetIndexBuffer( 0, ExtOutputBuffer );
SetIndexStyle( 0, DRAW_LINE, STYLE_SOLID, 2 );
SetIndexDrawBegin( 0, 2 * e_period );
g_period_minus_1=e_period - 1;
LOG_2=MathLog( 2.0 );
//----
return( 0 );
}
//+------------------------------------------------------------------+
//| FUNCTION : deinit |
//| Custor indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
return(0);
}
//+------------------------------------------------------------------+
//| FUNCTION : start |
//| This callback is fired by metatrader for each tick |
//+------------------------------------------------------------------+
int start()
{
int countedBars=IndicatorCounted();
//---- check for possible errors
if(countedBars < 0)
{
return(-1);
}
_computeLastNbBars( Bars - countedBars - 1 );
//----
return( 0 );
}
//+================================================================================================================+
//+=== FUNCTION : _computeLastNbBars ===+
//+=== ===+
//+=== ===+
//+=== This callback is fired by metatrader for each tick ===+
//+=== ===+
//+=== In : ===+
//+=== - lastBars : these "n" last bars must be repainted ===+
//+=== ===+
//+================================================================================================================+
//+------------------------------------------------------------------+
//| FUNCTION : _computeLastNbBars |
//| This callback is fired by metatrader for each tick |
//| In : - lastBars : these "n" last bars must be repainted |
//+------------------------------------------------------------------+
void _computeLastNbBars( int lastBars )
{
int pos;
switch( e_type_data )
{
case PRICE_CLOSE : _computeFRAMA( lastBars, Close ); break;
case PRICE_OPEN : _computeFRAMA( lastBars, Open ); break;
case PRICE_HIGH : _computeFRAMA( lastBars, High ); break;
case PRICE_LOW : _computeFRAMA( lastBars, Low ); break;

default :
Alert( "[ 20-ERROR " + FILENAME + " ] the imput parameter e_type_data <" + e_type_data + "> is unknown" );
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _computeFRASMA |
//| Compute the fractally modified SMA from input data. |
//| In : |
//| - lastBars : these "n" last bars must be repainted |
//| - inputData : data array on which the will be applied |
//| For technical explanations, see my blog: |
//| http://fractalfinance.blogspot.com/ |
//+------------------------------------------------------------------+
void _computeFRAMA( int lastBars, double inputData[] )
{
int pos, iteration;
double diff, priorDiff;
double length;
double priceMax, priceMin;
double fdi,alpha;
int speed;
//----
for( pos=lastBars; pos>=0; pos-- )
{
priceMax=_highest( e_period, pos, inputData );
priceMin=_lowest( e_period, pos, inputData );
length =0.0;
priorDiff=0.0;
//----
for( iteration=0; iteration <= g_period_minus_1; iteration++ )
{
if(( priceMax - priceMin)> 0.0 )
{
diff =(inputData[pos + iteration] - priceMin )/( priceMax - priceMin );
if(iteration > 0 )
{
length+=MathSqrt( MathPow( diff - priorDiff, 2.0)+(1.0/MathPow( e_period, 2.0)) );
}
priorDiff=diff;
}
}
if(length > 0.0 )
{
fdi=1.0 +(MathLog( length)+ LOG_2 )/MathLog( 2 * g_period_minus_1 );
}
else
{
/*
** The FDI algorithm suggests in this case a zero value.
** I prefer to use the previous FDI value.
*/
fdi=0.0;
}

alpha=MathExp(-4.6*(fdi-1)); // This is the recommendation from Elhers, but using fdi as the fractal dimension
ExtOutputBuffer[pos]=alpha*Close[pos]+(1-alpha)*ExtOutputBuffer[pos+1];
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _highest |
//| Search for the highest value in an array data |
//| In : |
//| - n : find the highest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value | |
//+------------------------------------------------------------------+
double _highest( int n, int pos, double inputData[] )
{
int length=pos + n;
double highest=0.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] > highest)highest=inputData[i];
}
return( highest );
}
//+------------------------------------------------------------------+
//| FUNCTION : _lowest | ===+
//| Search for the lowest value in an array data |
//| In : |
//| - n : find the hihest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value |
//+------------------------------------------------------------------+
double _lowest( int n, int pos, double inputData[] )
{
int length=pos + n;
double lowest=9999999999.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] < lowest)lowest=inputData[i];
}
return( lowest );
}
//+------------------------------------------------------------------+