Sorry for having been a bit absent these last few weeks, I am considering moving towards FX options trading, and I have therefore been studying this very different area.
This idea came to me quite accidentally. A few weeks ago, I bought "The blank swan" by Elie Ayache, out of curiosity really; I started reading it and after about 30 pages, even though, I got the gist of his ideas (which are more philosophical than technical), I nonetheless realized that I may enjoy the book more if I was a bit more knowledgeable in Options Trading. Until then, I had browsed through some mathematical finance books, but never went into much of the details.
I therefore did that and acquired Espen Gaarder Haug'"Derivatives: Models on Models", I am still reading it, but I already have realised how powerful Options trading can be.
As I see it, traders are to face two unknowns: the volatility and the direction of the move. So far, I don't think analytical tools provide for a very good prediction in terms of the direction, but I tend to think that volatility can be foreseen in a better way, albeit far from perfect.
Nonetheless, it is very possible to make money in Spot FX, the uncertainty about direction can indeed be compensated by a proper money management strategy (that can be found in many trading books, see those by Van Tharp for instance), but Options trading seems to be able to do that more efficiently by hedging the risk by means of a combination of options, diminishing thereby the exposure to direction while maintaining a profit potential out of the volatility variations. And this is only one aspect of Options Trading, as it appears to offer a rich range of other approaches to trading.
And last but not least, it also proposes rather stimulating intellectual challenges.
My knowledge of these combinations is still too incomplete for me to detail much more at this level, I shall therefore continue to explore this area in the next few weeks, and will confirm whether I chose to trade FX Options in the future. If so, one must expect some changes in the content of this blog, even though I will continue to look at technical tools to analyse the "underlying" time-series, I may concentrate as well on some portfolio strategy issues.
Thursday, July 1, 2010
Monday, May 17, 2010
Variation of the Hurst Exponent
While playing around with various strategies, I came to consider that an interesting way to use the fractal dimension is to look at its variations rather than its absolute value. Furthermore such an approach makes sense at a mathematical point of view: from equation (1) in this post, applying the functional power rule of derivation, we can see that:
}%20\right%20)}{\partial%20t}=Ht^{H-1}+\frac{\partial%20H}{\partial%20t}t^{H}ln(t)))
Rearranging it, we get:
![\frac{\partial \sigma}{\partial t}=t^{H-1}\left [ H+\frac{\partial H}{\partial t}tln(t) \right ]](http://latex.codecogs.com/gif.latex?\frac{\partial \sigma}{\partial t}=t^{H-1}\left [ H+\frac{\partial H}{\partial t}tln(t) \right ])
Asymptotically (for t sufficiently high), we can then see that the sign of the variation of H with time gives us the sign of the variation of the variance over time, and when this variation is positive, it indicates an increasing volatility and is therefore the best time to enter a trade. It must be noted that this indication does not say anything about the sense of the trade we should enter, and it therefore ought to be combined with a directional indicator in order to be fully operational.
Even though most of such variations can be seen by just looking at the FGDI graphic, it is just as easy (and possibly adding some precision) to program a new indicator that displays the variations of H over time, the script of this indicator can be found here on MQL4.
Below the indicator Hurst_Difference is displayed in the lower window on a 1hr chart for EUR/USD:

Whenever this indicator display a value above 0, it indicates a potential entry for a trade.
The parameters of Hurst_Difference.mq4 are:
f_period (integer): This is the period considered for calculating the fractal dimension, default is 30.
type_data (0,1,2,3,4,5 or 6): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW, 4=MEDIAN, 5=TYPICAL, 6=WEIGHTED), default is 0.
Rearranging it, we get:
Asymptotically (for t sufficiently high), we can then see that the sign of the variation of H with time gives us the sign of the variation of the variance over time, and when this variation is positive, it indicates an increasing volatility and is therefore the best time to enter a trade. It must be noted that this indication does not say anything about the sense of the trade we should enter, and it therefore ought to be combined with a directional indicator in order to be fully operational.
Even though most of such variations can be seen by just looking at the FGDI graphic, it is just as easy (and possibly adding some precision) to program a new indicator that displays the variations of H over time, the script of this indicator can be found here on MQL4.
Below the indicator Hurst_Difference is displayed in the lower window on a 1hr chart for EUR/USD:

Whenever this indicator display a value above 0, it indicates a potential entry for a trade.
The parameters of Hurst_Difference.mq4 are:
f_period (integer): This is the period considered for calculating the fractal dimension, default is 30.
type_data (0,1,2,3,4,5 or 6): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW, 4=MEDIAN, 5=TYPICAL, 6=WEIGHTED), default is 0.
Thursday, April 15, 2010
Self-similarity and a measure of it
Following an exchange via emails with a fellow trader, John Last, in which he made some remarks about the interest of some kind of self-similarity, I came to conceive a new indicator, which can be used to detect some convergence of behaviour between different timescales, in the sense outlined below.
____________________________________________________________________________________
I-General Remarks
Self-similarity is a well-known feature of fractals, it may however be useful to precise a few things about this concept.
The classic examples of fractals such as the Cantor Dust, the Von Koch Curve or the Sierpinski Gasket display an obvious self-similarity that is the direct consequence of their recursive mode of construction. However, when one comes to consider real-life applications of fractals, one should not expect to find such a perfect self-similarity.
Furthermore, when it comes to random fractals and their applications, which is the case of financial markets, self-similarity should not be taken as meaning a repetition of the exact same pattern, not even as a repetition of a pattern close enough to the original to warrant the use of "repetition".
Rather, what is meant in the case of financial price variations by self-similarity is really a "statistical self-similarity", which is more of a similarity of behavior between different timescales.
What should be compared therefore in order to measure the level of self-similarity at a given time, is not how the price curves at different timescales are "similar" to each others, but rather whether their behaviour, and particularly their volatility displays a level of self-similarity across timescales.
II-Dispersion of the Fractal Dimension across various timeframes
To measure this statistical similarity, I will only consider the dispersion between the FGDI of various timeframes around the FGDI of the longest timeframe considered.
For instance, considering the TimeFrame of 1hr, whose FGDI is fgdi(60), and the other shorter timeframes of 5mn (fgdi(5)), 15mn(fgdi(15)) and 30mn(fgdi(30)). The dispersion will be given by:
-fgdi(60))^{2}+(fgdi(15)-fgdi(60))^{2}+(fgdi(30)-fgdi(60))^{2}}{3}}\;\;\; \; \; (1))
Which is basically the formula of the standard deviation around the value of the longest timeframe.
This calculation seems rather straightforward, except that we must take care of a little technical problem: if, at the present instant, the value of the FGDI is actual for all the timeframes, the value of FGDI 30 bars ago in the 5mn timeframe is not corresponding to the value of the FGDI 30 bars ago in the 15mn timeframe. Indeed, the 30th bar back from now on the 5mn TF corresponds to 150mn ago, which on the 15mn timeframe corresponds to the 10th bar in the past.
Clearly therefore, to re-establish a correspondance that makes sense in equation (1) above, one must apply a change of index, whose general equation between a given timeframe (TF) and the reference timeframe (TFref) has the following form:
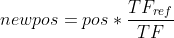
'newpos' is the new value of the index to be considered in the shorter timeframe in relation to the index 'pos' from the reference timeframe. Notice that in MQL4, the further a bar is in the past the higher is its index, in order to have the past index available, the main loop should be a decreasing one in terms of index, starting from as far as necessary in the past and calculating the bars towards the present.
That being said, I am aware, that the simplicity of this transformation does not ensure a perfect match between the different timeframes and an error of a few bars is still possible in the past, but the complexity of implementing a full check in order to ensure a perfect match is not warranted given that it will modify the final calculation in a negligible manner.
III-Implementation in MT4
I then wrote this indicator as MTF_FractalDispersion11.mq4, the script is available here, and here is what it looks like on a EUR/USD chart, in orange, in the bottom window:

For clarity purposes, the value of the dispersion is multiplied by 10, a low value is indicative of a high self-similarity, between the different timeframes.
For instance, in case of a trendy market (FGDI below 1.5), a low dispersion (corresponding to a high self-similarity) is a positive indicator to enter a trade in the sense of the trend, provided the said trend is in the same direction in all the timeframes considered.
The available timeframes are 5mn, 15mn, 30mn, 1hr, 4hr and 1 day. Each timeframe can be weighted as desired (but by an integer value).
Important remark:
From an excellent remark by John Last, I came to realise that the graphical representation of the Fractal dispersion is only aligned temporally to the prices graph (and therefore also to the Fractal Dimension graph) for the reference TimeFrame (the longest TF selected, with a weight above 0). On all the shorter TF, this representation will appear as contracted towards the right (proportionally to the distance we are looking at in the past from the present, rather than the Fractal Dispersion being contracted, it is the price, and therefore also the Fractal Dimension, that are dilated, taking more values than in the longer TF, within the same time interval), and the movements of the FractalDispersion will therefore appear to have taken place at a time later than at which they really did happen (the correct time will be the one displayed on the reference TF, i.e. the longest one selected).
The only time all the graphs will coincide on all TF is the present. Any analysis of the past should therefore take this into account.
This effect of contraction/dilatation is particularly well-illustrated on the following graph, sent to me, by John:

Here, by comparing the two lower windows (ignore the difference in numerical values, they are due to another mistake I did in the first version and that I also corrected), we see that the yellow curve MTF_FracDisp11 is nothing else than the contraction towards the left (with the present as the fixed point) of the green curve MTF_FracDisp.
Incidentally on this graph, the correct representation, except for a multiplicative factor of √2, is given by MTF_FracDisp, this is however exceptional and solely due to a specific setup, the 15mn TF is actually not the reference TF.
In all cases, MTF_FracDisp11 gives the proper value of the fractal dispersion and does coincide with the timescale only for the graph on the reference TF. And this indicator should only be used as such.
Notice that this indicator needs to access FGDI.mq4 on your PC, and that this one should therefore be present and compiled properly.
The parameters of MTF_FractalDispersion11.mq4 are:
e_period (integer): This is the period considered for calculating the fractal dimension, default is 30.
e_type_data (0,1,2,3,4,5 or 6): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW, 4=MEDIAN, 5=TYPICAL, 6=WEIGHTED), default is 0.
M5w (integer): This is the weight to be applied to the 5mn timeframe, default is 1.
M15w (integer): This is the weight to be applied to the 15mn timeframe, default is 1.
M30w (integer): This is the weight to be applied to the 30mn timeframe, default is 1.
M60w (integer): This is the weight to be applied to the 1hr timeframe, default is 1.
M240w (integer): This is the weight to be applied to the 4hr timeframe, default is 0.
M1440w (integer): This is the weight to be applied to the 1day timeframe, default is 0.
____________________________________________________________________________________
I-General Remarks
Self-similarity is a well-known feature of fractals, it may however be useful to precise a few things about this concept.
The classic examples of fractals such as the Cantor Dust, the Von Koch Curve or the Sierpinski Gasket display an obvious self-similarity that is the direct consequence of their recursive mode of construction. However, when one comes to consider real-life applications of fractals, one should not expect to find such a perfect self-similarity.
Furthermore, when it comes to random fractals and their applications, which is the case of financial markets, self-similarity should not be taken as meaning a repetition of the exact same pattern, not even as a repetition of a pattern close enough to the original to warrant the use of "repetition".
Rather, what is meant in the case of financial price variations by self-similarity is really a "statistical self-similarity", which is more of a similarity of behavior between different timescales.
What should be compared therefore in order to measure the level of self-similarity at a given time, is not how the price curves at different timescales are "similar" to each others, but rather whether their behaviour, and particularly their volatility displays a level of self-similarity across timescales.
II-Dispersion of the Fractal Dimension across various timeframes
To measure this statistical similarity, I will only consider the dispersion between the FGDI of various timeframes around the FGDI of the longest timeframe considered.
For instance, considering the TimeFrame of 1hr, whose FGDI is fgdi(60), and the other shorter timeframes of 5mn (fgdi(5)), 15mn(fgdi(15)) and 30mn(fgdi(30)). The dispersion will be given by:
Which is basically the formula of the standard deviation around the value of the longest timeframe.
This calculation seems rather straightforward, except that we must take care of a little technical problem: if, at the present instant, the value of the FGDI is actual for all the timeframes, the value of FGDI 30 bars ago in the 5mn timeframe is not corresponding to the value of the FGDI 30 bars ago in the 15mn timeframe. Indeed, the 30th bar back from now on the 5mn TF corresponds to 150mn ago, which on the 15mn timeframe corresponds to the 10th bar in the past.
Clearly therefore, to re-establish a correspondance that makes sense in equation (1) above, one must apply a change of index, whose general equation between a given timeframe (TF) and the reference timeframe (TFref) has the following form:
'newpos' is the new value of the index to be considered in the shorter timeframe in relation to the index 'pos' from the reference timeframe. Notice that in MQL4, the further a bar is in the past the higher is its index, in order to have the past index available, the main loop should be a decreasing one in terms of index, starting from as far as necessary in the past and calculating the bars towards the present.
That being said, I am aware, that the simplicity of this transformation does not ensure a perfect match between the different timeframes and an error of a few bars is still possible in the past, but the complexity of implementing a full check in order to ensure a perfect match is not warranted given that it will modify the final calculation in a negligible manner.
III-Implementation in MT4
I then wrote this indicator as MTF_FractalDispersion11.mq4, the script is available here, and here is what it looks like on a EUR/USD chart, in orange, in the bottom window:

For clarity purposes, the value of the dispersion is multiplied by 10, a low value is indicative of a high self-similarity, between the different timeframes.
For instance, in case of a trendy market (FGDI below 1.5), a low dispersion (corresponding to a high self-similarity) is a positive indicator to enter a trade in the sense of the trend, provided the said trend is in the same direction in all the timeframes considered.
The available timeframes are 5mn, 15mn, 30mn, 1hr, 4hr and 1 day. Each timeframe can be weighted as desired (but by an integer value).
Important remark:
From an excellent remark by John Last, I came to realise that the graphical representation of the Fractal dispersion is only aligned temporally to the prices graph (and therefore also to the Fractal Dimension graph) for the reference TimeFrame (the longest TF selected, with a weight above 0). On all the shorter TF, this representation will appear as contracted towards the right (proportionally to the distance we are looking at in the past from the present, rather than the Fractal Dispersion being contracted, it is the price, and therefore also the Fractal Dimension, that are dilated, taking more values than in the longer TF, within the same time interval), and the movements of the FractalDispersion will therefore appear to have taken place at a time later than at which they really did happen (the correct time will be the one displayed on the reference TF, i.e. the longest one selected).
The only time all the graphs will coincide on all TF is the present. Any analysis of the past should therefore take this into account.
This effect of contraction/dilatation is particularly well-illustrated on the following graph, sent to me, by John:

Here, by comparing the two lower windows (ignore the difference in numerical values, they are due to another mistake I did in the first version and that I also corrected), we see that the yellow curve MTF_FracDisp11 is nothing else than the contraction towards the left (with the present as the fixed point) of the green curve MTF_FracDisp.
Incidentally on this graph, the correct representation, except for a multiplicative factor of √2, is given by MTF_FracDisp, this is however exceptional and solely due to a specific setup, the 15mn TF is actually not the reference TF.
In all cases, MTF_FracDisp11 gives the proper value of the fractal dispersion and does coincide with the timescale only for the graph on the reference TF. And this indicator should only be used as such.
Notice that this indicator needs to access FGDI.mq4 on your PC, and that this one should therefore be present and compiled properly.
The parameters of MTF_FractalDispersion11.mq4 are:
e_period (integer): This is the period considered for calculating the fractal dimension, default is 30.
e_type_data (0,1,2,3,4,5 or 6): This is the type of price the indicator will consider (0=CLOSE, 1=OPEN, 2=HIGH, 3=LOW, 4=MEDIAN, 5=TYPICAL, 6=WEIGHTED), default is 0.
M5w (integer): This is the weight to be applied to the 5mn timeframe, default is 1.
M15w (integer): This is the weight to be applied to the 15mn timeframe, default is 1.
M30w (integer): This is the weight to be applied to the 30mn timeframe, default is 1.
M60w (integer): This is the weight to be applied to the 1hr timeframe, default is 1.
M240w (integer): This is the weight to be applied to the 4hr timeframe, default is 0.
M1440w (integer): This is the weight to be applied to the 1day timeframe, default is 0.
Saturday, February 6, 2010
Testing the Euro
It may be time for a little summary of how I see the fundamentals situation right now.
This past week has been a rich one in event on the EUR/USD front, we first saw the EUR rebounding from 1.385 to over 1.403, then back down to 1.365, all these moves being fed by news from the ECB supporting Greece, and worrying about Portugal, Italy and Spain.
The rebound has been discounted as a speculative action to the news of the ECB support to Greece, and the bubble has deflated as fast as it did inflate.
There was no real surprise in that, but the drop signals something bigger at play. This is the first big test ever for the Euro, and the fundamental question is: Will the ECB be able to impose a strict budget and economic policy to its member nations?
The way this question is answered will be important in the sense of establishing the status of the EUR as a serious reserve currency. As of now, this status is far from obtained yet, indeed, why didn't the EUR replace the USD as a safe haven currency?
Clearly, the social and political situation of Europe is relatively stable, the EUR currency is supported by the largest economy in the world, but the basic problem of the EUR is about sovereignty, political authority. If a single country had gathered the objective parameters that are behind the EUR, its currency would be the safe haven currency of the world. However, in the EU, there is not one single political voice, there is actually no clear warranty that all member countries will maintain their participation to the European framework if things turn bad. This ambiguity about the EUR is what, in my view, explains that it is, so far, not even considered as a potential reserve currency.
If something goes wrong with the USD, the US government is able to act upon it in a sovereign way, it can raise taxes or lower them as it deems fit. Nothing, within USA will oppose these decisions if they are clearly motivated by the defense of national interest, and the USD is doubtlessly considered as such.
The current crisis, in Greece, Portugal, Italy and especially Spain, will be the test for that. If it fails, if one of these countries strays away from abiding by the ECB recommendations, and somehow displays a lack of responsibility towards the other EU members, the EUR may not survive in its current form. On the other hand, if it succeeds, the EUR will have made a great leap towards being considered a reserve currency.
Meanwhile and according to the news about the troubled european countries and their interpretation, the EUR/USD pair should display high volatility with a medium-term down-trend, where I see the EUR retesting the low 20s.
This past week has been a rich one in event on the EUR/USD front, we first saw the EUR rebounding from 1.385 to over 1.403, then back down to 1.365, all these moves being fed by news from the ECB supporting Greece, and worrying about Portugal, Italy and Spain.
The rebound has been discounted as a speculative action to the news of the ECB support to Greece, and the bubble has deflated as fast as it did inflate.
There was no real surprise in that, but the drop signals something bigger at play. This is the first big test ever for the Euro, and the fundamental question is: Will the ECB be able to impose a strict budget and economic policy to its member nations?
The way this question is answered will be important in the sense of establishing the status of the EUR as a serious reserve currency. As of now, this status is far from obtained yet, indeed, why didn't the EUR replace the USD as a safe haven currency?
Clearly, the social and political situation of Europe is relatively stable, the EUR currency is supported by the largest economy in the world, but the basic problem of the EUR is about sovereignty, political authority. If a single country had gathered the objective parameters that are behind the EUR, its currency would be the safe haven currency of the world. However, in the EU, there is not one single political voice, there is actually no clear warranty that all member countries will maintain their participation to the European framework if things turn bad. This ambiguity about the EUR is what, in my view, explains that it is, so far, not even considered as a potential reserve currency.
If something goes wrong with the USD, the US government is able to act upon it in a sovereign way, it can raise taxes or lower them as it deems fit. Nothing, within USA will oppose these decisions if they are clearly motivated by the defense of national interest, and the USD is doubtlessly considered as such.
The current crisis, in Greece, Portugal, Italy and especially Spain, will be the test for that. If it fails, if one of these countries strays away from abiding by the ECB recommendations, and somehow displays a lack of responsibility towards the other EU members, the EUR may not survive in its current form. On the other hand, if it succeeds, the EUR will have made a great leap towards being considered a reserve currency.
Meanwhile and according to the news about the troubled european countries and their interpretation, the EUR/USD pair should display high volatility with a medium-term down-trend, where I see the EUR retesting the low 20s.
Subscribe to:
Posts (Atom)