In The Nature of Risk, Justin Mamis concludes his sixth chapter with the following remark:
Intuition, although seemingly spontaneous, apparently emotional, stems from a form of "information" that has become built-in from past experience. Discipline means choosing what to do unencumbered by the fear of making a mistake. Confidence means trusting our intuition that what we "see" is what we "know." There's no escaping to the external, to the objective, and no standing on the shaky ground of emotions. So the question becomes, How do we create within ourselves the heroic condition of confidence wherein risk is not danger but life.[MAM99, p.80]
The condition of confidence, heroic or not, to be actual, must somehow not deceive too much, and it would be naive to think that intuition never deceives us. Nonetheless, Mamis is right, intuition is a critical component in any decision process, not less in a trading context.
Technical analysis is very nice, but if fractal geometry teaches us anything, it is that we cannot foresee the evolution of complex processes on the basis of objective knowledge.
Now, if intuition deceives us, I contend that it is because it is trained to do so: Our whole education has conditioned us to think in deterministic terms, the analytical mind is praised and rewarded, hard sciences have simply excluded complex systems from their scope for centuries, and these systems are hardly touched at all in a normal education before a specialized Masters level even today.
Despite that, hard sciences and the mode of thinking they promote, are the foremost influence we are exposed to during our formal education. We are all members of the church of scientism, those who are not are likely to be members of churches even more deterministic than this one.
And our intuition follows this fold, even when we lack information to make a decision (which is almost always the case), we will tend to over-rely on the ones we have, and decide solely on this basis, extrapolating linearly from this partial knowledge, because we are conditioned to rely on linearity. We are simply unable to recognize, acknowledge and take into account the non-linearity of a process. It is this ability that must be developed over time, and it is this one that shall be called an efficient intuition.
There is one domain of the culture that may provide us with a way to build up this intuition, and that is Art. To each his own, personally, I am more sensitive to music and poetry, and it is therefore along these lines that I will argue my point, but I believe it can be transposed to other arts.
Adorno's critic of Schoenberg's and Stravinky's music links them both to the political and philosophical problematic of their times:
Art, indeed, always happens in a context, and relates to it in a very essential way, furthermore, it always takes on a problematic and resolve it figuratively. When Bartok or Stravinsky rejuvenated classical music with peasants songs, they merely reacted to the standardization of the world along western romanticist lines. But more than that, they provide us with a solution to the problematic of cosmopolitism, the native cultures don't have to be erased, they can be consolidated within an evolving culture (civilizations don't clash, they merge, sorry Mr.Huntington) and contribute to a manifold society (see the cosmopolitanist philosophy of Kwame Anthony Appiah for instance). The european empires could have used a bit of insight from them in the 20s and 30s.
And the same goes for today, here is a piece by Iannis Xenakis: Metastasis
The 1st and 3rd movement deals with a relativistic notion of time, that is a function of energy and mass. Interestingly, in trading, Mandelbrot defines the concept of trading time, which is also a function of what can be compared to energy and mass, and that is volume. That is actually a reflection of the dependence of the Hurst-Holder exponent to time [MAN97, pp39-40].
The second movement is even more interesting since it gives a musical translation of Fibonacci sequence.
Xenakis also wrote pieces dealing with Brownian Motion, Normal Distribution and Statistical Mechanics, all very interesting pieces. What they provide us with is an acquaintance that goes beyond the mere knowledge of well-defined criteria, an intuition that may articulate our decisions in a more efficient way.
Monday, January 26, 2009
Friday, January 23, 2009
The speed of the FRAMA (Part 1)
Earlier, I mentioned the logic behind the FRAMA (Fractal Adaptive Moving Average), and merely referred to John Ehlers'article. Here I wish to examine and discuss a bit more in detail this logic.
John Ehlers recommends to link the speed of an exponential moving average to the fractal dimension by making the coefficient α a function of this one via the following formula:
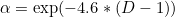
Let's accept this formula, in a first time, to consider the problematic of whether to apply this modification on an exponential moving average(EMA) or on a simple moving average(SMA).
The purpose of the EMA is to give more weight to the most recent price variations, this is a fair concern for the medium or long-term trader, I feel it is however a much less interesting feature for the intraday trader, who has to cope with a lot of noisy, meaningless fluctuations, and relies on the moving average precisely to avoid being distracted by this noise.
Besides, if we look at what happens for a high fractal dimension (approaching 2), the coefficient α is going to be very small (around 0.01, see the FRAMA article referenced earlier), the EMA will then be slowed down, but then, we also know that such a high fractal dimension coincides with the wildest noise, and therefore very high variations of prices. What is then the point of, on one hand slowing down the EMA, while this one will put a higher weight on the most recent, wildest price variations, thereby reflecting the wildness?
The two ideas clearly seem to conflict, and the resulting signal appears to be an ambiguous compromise where the exponential endeavors to speed up the moving average (by emphasizing the most recent variations) while the fractal dimension endeavors to slow it down.
I therefore prefer, especially as an intraday trader, to fractalise directly a SMA, and therefore get a direct and readable translation of the information implicit in the fractal dimension. This can be easily achieved by simply dividing the period of the SMA by the coefficient α.
Complement following a remark by Cool here:
In reply to Cool remark, here is a graph representing the FRAMA from Elhers in yellow, and this same FRAMA using a more precise calculation of the Fractal Dimension in red. Both FRAMA are exponential MA with a reference period of 10, their only difference is in the way the fractal dimension and therefore the coefficient α is calculated:
Yellow curve:
The fractal dimension is computed from the following equation:
-Log(N_{3})}{Log(2)})
where N1=(HighestPrice – LowestPrice) over the interval from 0 to T, divided by T, N2=(HighestPrice – LowestPrice) over the interval from T to 2T, divided by T and N3= (HighestPrice – LowestPrice) over the entire interval from 0 to 2T, divided by 2T
and
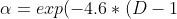))
Red Curve:
The fractal Dimension is computed from the following equation:
![D=1+\frac{Log[2\sum_{i=1}^{N}\sqrt{(\frac{close(i)-close(i-1)}{pricerange})^{2}+\frac{1}{N^{2}}}]}{Log(2N-2)}](http://latex.codecogs.com/gif.latex?D=1+\frac{Log[2\sum_{i=1}^{N}\sqrt{(\frac{close(i)-close(i-1)}{pricerange})^{2}+\frac{1}{N^{2}}}]}{Log(2N-2)})

Here are the two MT4 listings.
For the original Elhers FRAMA (Yellow Curve):
//+------------------------------------------------------------------+
//| FRAMA.mq4 |
//| Rosh |
//| http://www.alpari-idc.ru/ru/experts/articles/ |
//+------------------------------------------------------------------+
#property copyright "Rosh"
#property link "http://www.alpari-idc.ru/ru/experts/articles/"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_color1 DarkBlue
//---- input parameters
extern int PeriodFRAMA=10;
extern int PriceType=0;
//PRICE_CLOSE 0 Öåíà çàêðûòèÿ
//PRICE_OPEN 1 Öåíà îòêðûòèÿ
//PRICE_HIGH 2 Ìàêñèìàëüíàÿ öåíà
//PRICE_LOW 3 Ìèíèìàëüíàÿ öåíà
//PRICE_MEDIAN 4 Ñðåäíÿÿ öåíà, (high+low)/2
//PRICE_TYPICAL 5 Òèïè÷íàÿ öåíà, (high+low+close)/3
//PRICE_WEIGHTED 6 Âçâåøåííàÿ öåíà çàêðûòèÿ, (high+low+close+close)/4
//---- buffers
double ExtMapBuffer1[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function |
//+------------------------------------------------------------------+
int init()
{
//---- indicators
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,ExtMapBuffer1);
SetIndexEmptyValue(0,0.0);
//----
return(0);
}
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
//----
//----
return(0);
}
//+------------------------------------------------------------------+
//| âîçâðàùàåò öåíó |
//+------------------------------------------------------------------+
double Price(int shift)
{
//----
double res;
//----
switch (PriceType)
{
case PRICE_OPEN: res=Open[shift]; break;
case PRICE_HIGH: res=High[shift]; break;
case PRICE_LOW: res=Low[shift]; break;
case PRICE_MEDIAN: res=(High[shift]+Low[shift])/2.0; break;
case PRICE_TYPICAL: res=(High[shift]+Low[shift]+Close[shift])/3.0; break;
case PRICE_WEIGHTED: res=(High[shift]+Low[shift]+2*Close[shift])/4.0; break;
default: res=Close[shift];break;
}
return(res);
}
//+------------------------------------------------------------------+
//| Custom indicator iteration function |
//+------------------------------------------------------------------+
int start()
{
double Hi1,Lo1,Hi2,Lo2,Hi3,Lo3;
double N1,N2,N3,D;
double ALFA;
int limit;
int counted_bars=IndicatorCounted();
if (counted_bars==0) limit=Bars-2*PeriodFRAMA;
if (counted_bars>0) limit=Bars-counted_bars;
limit--;
//----
for (int i=limit;i>=0;i--)
{
Hi1=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i)];
Lo1=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i)];
Hi2=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i+PeriodFRAMA)];
Lo2=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i+PeriodFRAMA)];
Hi3=High[iHighest(Symbol(),0,MODE_HIGH,2*PeriodFRAMA,i)];
Lo3=Low[iLowest(Symbol(),0,MODE_LOW,2*PeriodFRAMA,i)];
N1=(Hi1-Lo1)/PeriodFRAMA;
N2=(Hi2-Lo2)/PeriodFRAMA;
N3=(Hi3-Lo3)/(2.0*PeriodFRAMA);
D=(MathLog(N1+N2)-MathLog(N3))/MathLog(2.0);
ALFA=MathExp(-4.6*(D-1.0));
ExtMapBuffer1[i]=ALFA*Price(i)+(1-ALFA)*ExtMapBuffer1[i+1];
}
//----
return(0);
}
//+------------------------------------------------------------------+
For the FRAMA modified with a different fractal dimension calculation (Red Curve):
//+------------------------------------------------------------------+
//| FRAMA2.mq4 |
//| Copyright © 2008, MetaQuotes Software Corp. |
//| http://www.metaquotes.net |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2008, MetaQuotes Software Corp."
#property link "http://www.metaquotes.net"
#property indicator_chart_window
#property indicator_color1 Red
#property indicator_width1 2
//************************************************************
// Input parameters
//************************************************************
extern int e_period =10;
extern int normal_speed =10;
extern int e_type_data =PRICE_CLOSE;
//************************************************************
// Constant
//************************************************************
string INDICATOR_NAME="FRAMA2";
string FILENAME ="FRAMA2.mq4";
double LOG_2;
//************************************************************
// Private vars
//************************************************************
double ExtOutputBuffer[];
int g_period_minus_1;
//+-----------------------------------------------------------------------+
//| FUNCTION : init |
//| Initialization function |
//| Check the user input parameters and convert them in appropriate types.|
//+-----------------------------------------------------------------------+
int init()
{
// Check e_period input parameter
if(e_period < 2 )
{
Alert( "[ 10-ERROR " + FILENAME + " ] input parameter \"e_period\" must be >= 1 (" + e_period + ")" );
return( -1 );
}
if(e_type_data < PRICE_CLOSE || e_type_data > PRICE_WEIGHTED )
{
Alert( "[ 20-ERROR " + FILENAME + " ] input parameter \"e_type_data\" unknown (" + e_type_data + ")" );
return( -1 );
}
IndicatorBuffers( 1 );
SetIndexBuffer( 0, ExtOutputBuffer );
SetIndexStyle( 0, DRAW_LINE, STYLE_SOLID, 2 );
SetIndexDrawBegin( 0, 2 * e_period );
g_period_minus_1=e_period - 1;
LOG_2=MathLog( 2.0 );
//----
return( 0 );
}
//+------------------------------------------------------------------+
//| FUNCTION : deinit |
//| Custor indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
return(0);
}
//+------------------------------------------------------------------+
//| FUNCTION : start |
//| This callback is fired by metatrader for each tick |
//+------------------------------------------------------------------+
int start()
{
int countedBars=IndicatorCounted();
//---- check for possible errors
if(countedBars < 0)
{
return(-1);
}
_computeLastNbBars( Bars - countedBars - 1 );
//----
return( 0 );
}
//+================================================================================================================+
//+=== FUNCTION : _computeLastNbBars ===+
//+=== ===+
//+=== ===+
//+=== This callback is fired by metatrader for each tick ===+
//+=== ===+
//+=== In : ===+
//+=== - lastBars : these "n" last bars must be repainted ===+
//+=== ===+
//+================================================================================================================+
//+------------------------------------------------------------------+
//| FUNCTION : _computeLastNbBars |
//| This callback is fired by metatrader for each tick |
//| In : - lastBars : these "n" last bars must be repainted |
//+------------------------------------------------------------------+
void _computeLastNbBars( int lastBars )
{
int pos;
switch( e_type_data )
{
case PRICE_CLOSE : _computeFRAMA( lastBars, Close ); break;
case PRICE_OPEN : _computeFRAMA( lastBars, Open ); break;
case PRICE_HIGH : _computeFRAMA( lastBars, High ); break;
case PRICE_LOW : _computeFRAMA( lastBars, Low ); break;
default :
Alert( "[ 20-ERROR " + FILENAME + " ] the imput parameter e_type_data <" + e_type_data + "> is unknown" );
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _computeFRASMA |
//| Compute the fractally modified SMA from input data. |
//| In : |
//| - lastBars : these "n" last bars must be repainted |
//| - inputData : data array on which the will be applied |
//| For technical explanations, see my blog: |
//| http://fractalfinance.blogspot.com/ |
//+------------------------------------------------------------------+
void _computeFRAMA( int lastBars, double inputData[] )
{
int pos, iteration;
double diff, priorDiff;
double length;
double priceMax, priceMin;
double fdi,alpha;
int speed;
//----
for( pos=lastBars; pos>=0; pos-- )
{
priceMax=_highest( e_period, pos, inputData );
priceMin=_lowest( e_period, pos, inputData );
length =0.0;
priorDiff=0.0;
//----
for( iteration=0; iteration <= g_period_minus_1; iteration++ )
{
if(( priceMax - priceMin)> 0.0 )
{
diff =(inputData[pos + iteration] - priceMin )/( priceMax - priceMin );
if(iteration > 0 )
{
length+=MathSqrt( MathPow( diff - priorDiff, 2.0)+(1.0/MathPow( e_period, 2.0)) );
}
priorDiff=diff;
}
}
if(length > 0.0 )
{
fdi=1.0 +(MathLog( length)+ LOG_2 )/MathLog( 2 * g_period_minus_1 );
}
else
{
/*
** The FDI algorithm suggests in this case a zero value.
** I prefer to use the previous FDI value.
*/
fdi=0.0;
}
alpha=MathExp(-4.6*(fdi-1)); // This is the recommendation from Elhers, but using fdi as the fractal dimension
ExtOutputBuffer[pos]=alpha*Close[pos]+(1-alpha)*ExtOutputBuffer[pos+1];
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _highest |
//| Search for the highest value in an array data |
//| In : |
//| - n : find the highest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value | |
//+------------------------------------------------------------------+
double _highest( int n, int pos, double inputData[] )
{
int length=pos + n;
double highest=0.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] > highest)highest=inputData[i];
}
return( highest );
}
//+------------------------------------------------------------------+
//| FUNCTION : _lowest | ===+
//| Search for the lowest value in an array data |
//| In : |
//| - n : find the hihest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value |
//+------------------------------------------------------------------+
double _lowest( int n, int pos, double inputData[] )
{
int length=pos + n;
double lowest=9999999999.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] < lowest)lowest=inputData[i];
}
return( lowest );
}
//+------------------------------------------------------------------+
John Ehlers recommends to link the speed of an exponential moving average to the fractal dimension by making the coefficient α a function of this one via the following formula:
Let's accept this formula, in a first time, to consider the problematic of whether to apply this modification on an exponential moving average(EMA) or on a simple moving average(SMA).
The purpose of the EMA is to give more weight to the most recent price variations, this is a fair concern for the medium or long-term trader, I feel it is however a much less interesting feature for the intraday trader, who has to cope with a lot of noisy, meaningless fluctuations, and relies on the moving average precisely to avoid being distracted by this noise.
Besides, if we look at what happens for a high fractal dimension (approaching 2), the coefficient α is going to be very small (around 0.01, see the FRAMA article referenced earlier), the EMA will then be slowed down, but then, we also know that such a high fractal dimension coincides with the wildest noise, and therefore very high variations of prices. What is then the point of, on one hand slowing down the EMA, while this one will put a higher weight on the most recent, wildest price variations, thereby reflecting the wildness?
The two ideas clearly seem to conflict, and the resulting signal appears to be an ambiguous compromise where the exponential endeavors to speed up the moving average (by emphasizing the most recent variations) while the fractal dimension endeavors to slow it down.
I therefore prefer, especially as an intraday trader, to fractalise directly a SMA, and therefore get a direct and readable translation of the information implicit in the fractal dimension. This can be easily achieved by simply dividing the period of the SMA by the coefficient α.
Complement following a remark by Cool here:
In reply to Cool remark, here is a graph representing the FRAMA from Elhers in yellow, and this same FRAMA using a more precise calculation of the Fractal Dimension in red. Both FRAMA are exponential MA with a reference period of 10, their only difference is in the way the fractal dimension and therefore the coefficient α is calculated:
Yellow curve:
The fractal dimension is computed from the following equation:
where N1=(HighestPrice – LowestPrice) over the interval from 0 to T, divided by T, N2=(HighestPrice – LowestPrice) over the interval from T to 2T, divided by T and N3= (HighestPrice – LowestPrice) over the entire interval from 0 to 2T, divided by 2T
and
Red Curve:
The fractal Dimension is computed from the following equation:

Here are the two MT4 listings.
For the original Elhers FRAMA (Yellow Curve):
//+------------------------------------------------------------------+
//| FRAMA.mq4 |
//| Rosh |
//| http://www.alpari-idc.ru/ru/experts/articles/ |
//+------------------------------------------------------------------+
#property copyright "Rosh"
#property link "http://www.alpari-idc.ru/ru/experts/articles/"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_color1 DarkBlue
//---- input parameters
extern int PeriodFRAMA=10;
extern int PriceType=0;
//PRICE_CLOSE 0 Öåíà çàêðûòèÿ
//PRICE_OPEN 1 Öåíà îòêðûòèÿ
//PRICE_HIGH 2 Ìàêñèìàëüíàÿ öåíà
//PRICE_LOW 3 Ìèíèìàëüíàÿ öåíà
//PRICE_MEDIAN 4 Ñðåäíÿÿ öåíà, (high+low)/2
//PRICE_TYPICAL 5 Òèïè÷íàÿ öåíà, (high+low+close)/3
//PRICE_WEIGHTED 6 Âçâåøåííàÿ öåíà çàêðûòèÿ, (high+low+close+close)/4
//---- buffers
double ExtMapBuffer1[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function |
//+------------------------------------------------------------------+
int init()
{
//---- indicators
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,ExtMapBuffer1);
SetIndexEmptyValue(0,0.0);
//----
return(0);
}
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
//----
//----
return(0);
}
//+------------------------------------------------------------------+
//| âîçâðàùàåò öåíó |
//+------------------------------------------------------------------+
double Price(int shift)
{
//----
double res;
//----
switch (PriceType)
{
case PRICE_OPEN: res=Open[shift]; break;
case PRICE_HIGH: res=High[shift]; break;
case PRICE_LOW: res=Low[shift]; break;
case PRICE_MEDIAN: res=(High[shift]+Low[shift])/2.0; break;
case PRICE_TYPICAL: res=(High[shift]+Low[shift]+Close[shift])/3.0; break;
case PRICE_WEIGHTED: res=(High[shift]+Low[shift]+2*Close[shift])/4.0; break;
default: res=Close[shift];break;
}
return(res);
}
//+------------------------------------------------------------------+
//| Custom indicator iteration function |
//+------------------------------------------------------------------+
int start()
{
double Hi1,Lo1,Hi2,Lo2,Hi3,Lo3;
double N1,N2,N3,D;
double ALFA;
int limit;
int counted_bars=IndicatorCounted();
if (counted_bars==0) limit=Bars-2*PeriodFRAMA;
if (counted_bars>0) limit=Bars-counted_bars;
limit--;
//----
for (int i=limit;i>=0;i--)
{
Hi1=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i)];
Lo1=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i)];
Hi2=High[iHighest(Symbol(),0,MODE_HIGH,PeriodFRAMA,i+PeriodFRAMA)];
Lo2=Low[iLowest(Symbol(),0,MODE_LOW,PeriodFRAMA,i+PeriodFRAMA)];
Hi3=High[iHighest(Symbol(),0,MODE_HIGH,2*PeriodFRAMA,i)];
Lo3=Low[iLowest(Symbol(),0,MODE_LOW,2*PeriodFRAMA,i)];
N1=(Hi1-Lo1)/PeriodFRAMA;
N2=(Hi2-Lo2)/PeriodFRAMA;
N3=(Hi3-Lo3)/(2.0*PeriodFRAMA);
D=(MathLog(N1+N2)-MathLog(N3))/MathLog(2.0);
ALFA=MathExp(-4.6*(D-1.0));
ExtMapBuffer1[i]=ALFA*Price(i)+(1-ALFA)*ExtMapBuffer1[i+1];
}
//----
return(0);
}
//+------------------------------------------------------------------+
For the FRAMA modified with a different fractal dimension calculation (Red Curve):
//+------------------------------------------------------------------+
//| FRAMA2.mq4 |
//| Copyright © 2008, MetaQuotes Software Corp. |
//| http://www.metaquotes.net |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2008, MetaQuotes Software Corp."
#property link "http://www.metaquotes.net"
#property indicator_chart_window
#property indicator_color1 Red
#property indicator_width1 2
//************************************************************
// Input parameters
//************************************************************
extern int e_period =10;
extern int normal_speed =10;
extern int e_type_data =PRICE_CLOSE;
//************************************************************
// Constant
//************************************************************
string INDICATOR_NAME="FRAMA2";
string FILENAME ="FRAMA2.mq4";
double LOG_2;
//************************************************************
// Private vars
//************************************************************
double ExtOutputBuffer[];
int g_period_minus_1;
//+-----------------------------------------------------------------------+
//| FUNCTION : init |
//| Initialization function |
//| Check the user input parameters and convert them in appropriate types.|
//+-----------------------------------------------------------------------+
int init()
{
// Check e_period input parameter
if(e_period < 2 )
{
Alert( "[ 10-ERROR " + FILENAME + " ] input parameter \"e_period\" must be >= 1 (" + e_period + ")" );
return( -1 );
}
if(e_type_data < PRICE_CLOSE || e_type_data > PRICE_WEIGHTED )
{
Alert( "[ 20-ERROR " + FILENAME + " ] input parameter \"e_type_data\" unknown (" + e_type_data + ")" );
return( -1 );
}
IndicatorBuffers( 1 );
SetIndexBuffer( 0, ExtOutputBuffer );
SetIndexStyle( 0, DRAW_LINE, STYLE_SOLID, 2 );
SetIndexDrawBegin( 0, 2 * e_period );
g_period_minus_1=e_period - 1;
LOG_2=MathLog( 2.0 );
//----
return( 0 );
}
//+------------------------------------------------------------------+
//| FUNCTION : deinit |
//| Custor indicator deinitialization function |
//+------------------------------------------------------------------+
int deinit()
{
return(0);
}
//+------------------------------------------------------------------+
//| FUNCTION : start |
//| This callback is fired by metatrader for each tick |
//+------------------------------------------------------------------+
int start()
{
int countedBars=IndicatorCounted();
//---- check for possible errors
if(countedBars < 0)
{
return(-1);
}
_computeLastNbBars( Bars - countedBars - 1 );
//----
return( 0 );
}
//+================================================================================================================+
//+=== FUNCTION : _computeLastNbBars ===+
//+=== ===+
//+=== ===+
//+=== This callback is fired by metatrader for each tick ===+
//+=== ===+
//+=== In : ===+
//+=== - lastBars : these "n" last bars must be repainted ===+
//+=== ===+
//+================================================================================================================+
//+------------------------------------------------------------------+
//| FUNCTION : _computeLastNbBars |
//| This callback is fired by metatrader for each tick |
//| In : - lastBars : these "n" last bars must be repainted |
//+------------------------------------------------------------------+
void _computeLastNbBars( int lastBars )
{
int pos;
switch( e_type_data )
{
case PRICE_CLOSE : _computeFRAMA( lastBars, Close ); break;
case PRICE_OPEN : _computeFRAMA( lastBars, Open ); break;
case PRICE_HIGH : _computeFRAMA( lastBars, High ); break;
case PRICE_LOW : _computeFRAMA( lastBars, Low ); break;
default :
Alert( "[ 20-ERROR " + FILENAME + " ] the imput parameter e_type_data <" + e_type_data + "> is unknown" );
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _computeFRASMA |
//| Compute the fractally modified SMA from input data. |
//| In : |
//| - lastBars : these "n" last bars must be repainted |
//| - inputData : data array on which the will be applied |
//| For technical explanations, see my blog: |
//| http://fractalfinance.blogspot.com/ |
//+------------------------------------------------------------------+
void _computeFRAMA( int lastBars, double inputData[] )
{
int pos, iteration;
double diff, priorDiff;
double length;
double priceMax, priceMin;
double fdi,alpha;
int speed;
//----
for( pos=lastBars; pos>=0; pos-- )
{
priceMax=_highest( e_period, pos, inputData );
priceMin=_lowest( e_period, pos, inputData );
length =0.0;
priorDiff=0.0;
//----
for( iteration=0; iteration <= g_period_minus_1; iteration++ )
{
if(( priceMax - priceMin)> 0.0 )
{
diff =(inputData[pos + iteration] - priceMin )/( priceMax - priceMin );
if(iteration > 0 )
{
length+=MathSqrt( MathPow( diff - priorDiff, 2.0)+(1.0/MathPow( e_period, 2.0)) );
}
priorDiff=diff;
}
}
if(length > 0.0 )
{
fdi=1.0 +(MathLog( length)+ LOG_2 )/MathLog( 2 * g_period_minus_1 );
}
else
{
/*
** The FDI algorithm suggests in this case a zero value.
** I prefer to use the previous FDI value.
*/
fdi=0.0;
}
alpha=MathExp(-4.6*(fdi-1)); // This is the recommendation from Elhers, but using fdi as the fractal dimension
ExtOutputBuffer[pos]=alpha*Close[pos]+(1-alpha)*ExtOutputBuffer[pos+1];
}
}
//+------------------------------------------------------------------+
//| FUNCTION : _highest |
//| Search for the highest value in an array data |
//| In : |
//| - n : find the highest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value | |
//+------------------------------------------------------------------+
double _highest( int n, int pos, double inputData[] )
{
int length=pos + n;
double highest=0.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] > highest)highest=inputData[i];
}
return( highest );
}
//+------------------------------------------------------------------+
//| FUNCTION : _lowest | ===+
//| Search for the lowest value in an array data |
//| In : |
//| - n : find the hihest on these n data |
//| - pos : begin to search for from this index |
//| - inputData : data array on which the searching for is done |
//| |
//| Return : the highest value |
//+------------------------------------------------------------------+
double _lowest( int n, int pos, double inputData[] )
{
int length=pos + n;
double lowest=9999999999.0;
//----
for( int i=pos; i < length; i++ )
{
if(inputData[i] < lowest)lowest=inputData[i];
}
return( lowest );
}
//+------------------------------------------------------------------+
Saturday, January 17, 2009
Baroque revival
Europa Galante and Fabio Biondi are re-inventing (or re-discovering, or both) Baroque Music. Judge for yourself:
Their style is controversial, Biondi is sometimes dismissed as an over-doer (but isn't it in the spirit of the baroque ?), but there is a genuine experimental aspect to his work, backed by serious musicological researches; and the result, to me at least, is both enjoyable and interesting.
Their style is controversial, Biondi is sometimes dismissed as an over-doer (but isn't it in the spirit of the baroque ?), but there is a genuine experimental aspect to his work, backed by serious musicological researches; and the result, to me at least, is both enjoyable and interesting.
Subscribe to:
Posts (Atom)