In relation to my last post, about the "flapping butterflies", a discussion is going on between myself and Duc on his site, it takes place over several posts, so a bit difficult to follow, but in case some of my readers are interested.
Also, I updated the format of comments here, so that, anybody can now post one, even as anonymous if one wishes. I actually did not realize earlier that there was some limitations on this.
Wednesday, February 25, 2009
Saturday, February 21, 2009
Flapping butterflies don't make hurricanes (A critical view of the 2008-2009 crisis)
Many analysts have provided, are providing, and will provide still for some time with explanations of the current crisis, and often conclude by sketching some remedies to it, or at least which system should be implemented in the future to avert a similar situation. I seldom totally disagree with those explanations, but I even more rarely totally agree with them, and I almost never share their sketches of a solution.
Ultimately though, I think the core problem is seldom touched at all.
As for the elements commonly incriminated for the crisis, here are a few in no order:
- CDS and their unregulated practice
- SubPrime loans and their securitization
- Expansionary monetary policy of the central banks (primarily the one from USA)
- Intervention of the US government to promote access to home ownership (primarily the Community Reinvestment Act)
- The carelessness of the Credit Ratings Agencies
- The dogmatic culture in financial mathematics (relying on a Gaussian model) that promoted risky strategy by presenting them as riskless
- American over-consumerism and over-reliance on credit
...etc.
According to the analyst, some of these phenomena will be emphasized, others may simply be ignored or neglected, but each will be weighted in order to rationalize a judgment that often appears to have preexisted to a fair analysis, and the rhetorics betrays more or less clearly a whole set of prejudices that is not very difficult to relate to a school of economics.
It is clear to me that all these elements (and many others) have played a role at one time or another in the unfolding of the crisis, it is however very difficult and hazardous to identify their relative importance.
Rather than contributing to this debate by merely adding my own prejudices and rationalization, I will try here to bring up a few elements that I have not seen often mentioned (if at all).
1)I saw many who tried to put the key responsibility of the crisis on government intervention, some defending the point that in absence of such intervention, crisis would simply not develop at all, at least not up to any significant level. This idea is simply false and has been demonstrated to be so in 1966 by Mandelbrot in an article[1], reprinted as the chapter E19 in [MAN97]. In the reprint, Mandelbrot includes the following foreword:
In there, Mandelbrot demonstrates how speculative bubbles do occur "naturally" in a market. While it is very possible that some interventions will facilitate bubbles, this mere possibility allows for the opposite one, that some intervention can also diminish the intensity of bubbles, and even prevent their apparition or their violent burst.
The prejudice that roots speculative bubbles in government intervention (read as disturbances of a market otherwise well-balanced) is untenable.
2)One reading of this crisis can be that of the failure of dynamic hedging. I can't testify about the importance of this failure and its relevance in this crisis, but if I am to believe Espen Gaarder Haug and Nassim Nicholas Taleb in this article[2], and if dynamic hedging was used in any systematic way by the main financial institutions, there is certainly some kind of responsibility to be found here.
At the root of the popularity of dynamic hedging, there is again the dogma that markets are inherently Gaussian, and eventually do not derive into fat-tailed behavior (where serious bubbles form and burst). This is obviously a denial of the reality of their nature, a nature that has been largely documented over the last 40 years, and clearly displays a chaotic behavior.
3)Another type of analysts, while recognizing the correctness of the occurrence of crisis in an unhampered market, will argue that any intervention can only make things worse, human minds simply cannot understand the full effect of their actions, and in a complex system such as the economy, they better abstain from any attempt to act.
I can't help seeing the fundamentally religious mindset behind such a position, in that it hypostasizes the market into an order beyond human understanding, that seems to exist in a transcendental realm: From a mere metaphor, the "invisible hand" suddenly becomes the Logos, the infallible organizing principle.
This rationale though, hinges on a misunderstanding of the "Butterfly Effect". This famous effect is known by most, and for most, it is the only thing they know about Chaos Theory (and Fractals), and the dynamics of complex systems, but no butterfly ever created a hurricane, the image is simply that, again, a metaphor to say that very slight disturbance may contribute to(rather than create) unforeseen catastrophic effect. It does not mean that they always do so, or even that human understanding cannot have any control over the most adverse of these effects. Real complex systems have some level of tolerance, of self-regulation at a local level, of resilience (to use a fashionable term). We may not control the weather, but we can open an umbrella not to get wet when it rains, and it does not make the rain any heavier.
Human beings are acting, whether in relation to the weather or in relation to the market, there is no such thing as an unhampered market, because there is no such a thing as a market without human actions.
The question is whether we should think those interventions in a rational manner, from a social point of view, or whether we should leave each individuals to impose themselves in the market on the basis of their luck, intelligence and birth, and let the big picture to the care of the "invisible hand" (if one has faith in its omnipotence, with regard to this context, this faith anyway falls beyond rationality).
In conclusion, let me expose my opinion, which may be prejudiced, but if so, I welcome any criticism of it.
I see the root of the current crisis in this core belief, of a religious nature, about the market (as self-regulated by the "invisible hand"), that led many people to ignore what the market really was, because it was inconvenient for them to acknowledge it (its chaotic nature was going against the belief).
The origin of this credo can be found in the Cold War (which provided a propitious intellectual climate for such a faith to flourish: Against the religious socialism of the communist block, a religious form of capitalism was seen as most welcome), and more precisely in the Neo-conservative ideology that succeeded to fusion several elements of economic thought mostly coming from the Austrian school, Monetarism and Libertarianism; it further blended these elements with the US christian movements that spread from (or were heavily influenced by) Calvinism, Pietism, Methodism and Baptism (cf. Max Weber[3] about the historical link between protestant sects and Capitalism).
As a result, a very dogmatic and religious ideology came into play as the official economic philosophy of american politics (beyond traditional party lines) and even found strong supporters in western Europe (until recently, Sarkozy and Berlusconi were among them). It found its natural expression in a minimization and constant undermining of political power (and of the legitimacy of democracy, and therefore of democratic intervention), to the profit of economic institutions (not submitted to the control of the public in any way) and capitalist actors, the latter often providing the very people in control of the former, a kind of crony "democracy" and neocorporatism (very much acquainted with its fascistic counterpart) developed on this basis. This phenomenon is well documented, as early as the late 80s by Habermas in Ecrits Politiques[4] (sorry, I don't know the english version or even whether there is one).
It is eventually this ideology that I will rank as holding the primary responsibility for the current situation; and one may still see its influence at work in the ways the crisis is analysed, and recommendations are made to decrease even more the influence of the government in the economic realm.
References:
[1]: Forecasts of Future Prices, Unbiased Markets, and "Martingale" Models
[2]: Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula
[3]: The Protestant Ethic and the Spirit of Capitalism
[4]: Ecrits politiques
Ultimately though, I think the core problem is seldom touched at all.
As for the elements commonly incriminated for the crisis, here are a few in no order:
- CDS and their unregulated practice
- SubPrime loans and their securitization
- Expansionary monetary policy of the central banks (primarily the one from USA)
- Intervention of the US government to promote access to home ownership (primarily the Community Reinvestment Act)
- The carelessness of the Credit Ratings Agencies
- The dogmatic culture in financial mathematics (relying on a Gaussian model) that promoted risky strategy by presenting them as riskless
- American over-consumerism and over-reliance on credit
...etc.
According to the analyst, some of these phenomena will be emphasized, others may simply be ignored or neglected, but each will be weighted in order to rationalize a judgment that often appears to have preexisted to a fair analysis, and the rhetorics betrays more or less clearly a whole set of prejudices that is not very difficult to relate to a school of economics.
It is clear to me that all these elements (and many others) have played a role at one time or another in the unfolding of the crisis, it is however very difficult and hazardous to identify their relative importance.
Rather than contributing to this debate by merely adding my own prejudices and rationalization, I will try here to bring up a few elements that I have not seen often mentioned (if at all).
1)I saw many who tried to put the key responsibility of the crisis on government intervention, some defending the point that in absence of such intervention, crisis would simply not develop at all, at least not up to any significant level. This idea is simply false and has been demonstrated to be so in 1966 by Mandelbrot in an article[1], reprinted as the chapter E19 in [MAN97]. In the reprint, Mandelbrot includes the following foreword:
Two terms are found in the title of this reprint, but not of the originals, namely "nonlinear" and "rational bubble". They express the two main points of this paper in words that were not available to me in 1966.
The main substantive finding was that rational behavior on the part of the market may lead to "wild" speculative bubble(...). The randomness of these bubble is called "wild" in my present vocabulary, because they can be extremely large, and their sizes and duration follow a scaling distribution. This distribution is closely akin to the L-stable distribution introduced in the model of price variation presented in M 1963b.
In there, Mandelbrot demonstrates how speculative bubbles do occur "naturally" in a market. While it is very possible that some interventions will facilitate bubbles, this mere possibility allows for the opposite one, that some intervention can also diminish the intensity of bubbles, and even prevent their apparition or their violent burst.
The prejudice that roots speculative bubbles in government intervention (read as disturbances of a market otherwise well-balanced) is untenable.
2)One reading of this crisis can be that of the failure of dynamic hedging. I can't testify about the importance of this failure and its relevance in this crisis, but if I am to believe Espen Gaarder Haug and Nassim Nicholas Taleb in this article[2], and if dynamic hedging was used in any systematic way by the main financial institutions, there is certainly some kind of responsibility to be found here.
At the root of the popularity of dynamic hedging, there is again the dogma that markets are inherently Gaussian, and eventually do not derive into fat-tailed behavior (where serious bubbles form and burst). This is obviously a denial of the reality of their nature, a nature that has been largely documented over the last 40 years, and clearly displays a chaotic behavior.
3)Another type of analysts, while recognizing the correctness of the occurrence of crisis in an unhampered market, will argue that any intervention can only make things worse, human minds simply cannot understand the full effect of their actions, and in a complex system such as the economy, they better abstain from any attempt to act.
I can't help seeing the fundamentally religious mindset behind such a position, in that it hypostasizes the market into an order beyond human understanding, that seems to exist in a transcendental realm: From a mere metaphor, the "invisible hand" suddenly becomes the Logos, the infallible organizing principle.
This rationale though, hinges on a misunderstanding of the "Butterfly Effect". This famous effect is known by most, and for most, it is the only thing they know about Chaos Theory (and Fractals), and the dynamics of complex systems, but no butterfly ever created a hurricane, the image is simply that, again, a metaphor to say that very slight disturbance may contribute to(rather than create) unforeseen catastrophic effect. It does not mean that they always do so, or even that human understanding cannot have any control over the most adverse of these effects. Real complex systems have some level of tolerance, of self-regulation at a local level, of resilience (to use a fashionable term). We may not control the weather, but we can open an umbrella not to get wet when it rains, and it does not make the rain any heavier.
Human beings are acting, whether in relation to the weather or in relation to the market, there is no such thing as an unhampered market, because there is no such a thing as a market without human actions.
The question is whether we should think those interventions in a rational manner, from a social point of view, or whether we should leave each individuals to impose themselves in the market on the basis of their luck, intelligence and birth, and let the big picture to the care of the "invisible hand" (if one has faith in its omnipotence, with regard to this context, this faith anyway falls beyond rationality).
In conclusion, let me expose my opinion, which may be prejudiced, but if so, I welcome any criticism of it.
I see the root of the current crisis in this core belief, of a religious nature, about the market (as self-regulated by the "invisible hand"), that led many people to ignore what the market really was, because it was inconvenient for them to acknowledge it (its chaotic nature was going against the belief).
The origin of this credo can be found in the Cold War (which provided a propitious intellectual climate for such a faith to flourish: Against the religious socialism of the communist block, a religious form of capitalism was seen as most welcome), and more precisely in the Neo-conservative ideology that succeeded to fusion several elements of economic thought mostly coming from the Austrian school, Monetarism and Libertarianism; it further blended these elements with the US christian movements that spread from (or were heavily influenced by) Calvinism, Pietism, Methodism and Baptism (cf. Max Weber[3] about the historical link between protestant sects and Capitalism).
As a result, a very dogmatic and religious ideology came into play as the official economic philosophy of american politics (beyond traditional party lines) and even found strong supporters in western Europe (until recently, Sarkozy and Berlusconi were among them). It found its natural expression in a minimization and constant undermining of political power (and of the legitimacy of democracy, and therefore of democratic intervention), to the profit of economic institutions (not submitted to the control of the public in any way) and capitalist actors, the latter often providing the very people in control of the former, a kind of crony "democracy" and neocorporatism (very much acquainted with its fascistic counterpart) developed on this basis. This phenomenon is well documented, as early as the late 80s by Habermas in Ecrits Politiques[4] (sorry, I don't know the english version or even whether there is one).
It is eventually this ideology that I will rank as holding the primary responsibility for the current situation; and one may still see its influence at work in the ways the crisis is analysed, and recommendations are made to decrease even more the influence of the government in the economic realm.
References:
[1]: Forecasts of Future Prices, Unbiased Markets, and "Martingale" Models
[2]: Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula
[3]: The Protestant Ethic and the Spirit of Capitalism
[4]: Ecrits politiques
Sunday, February 15, 2009
The speed of the FRAMA (Part 2): The FRASMA
Having explained my preference for a "fractalisation" of the MA to apply on a SMA(rather than on an EMA), I shall now discuss the exact form of this "fractalisation".
A modification, close to the one recommended by Ehlers, would be to merely divide the period of the SMA by the coefficient α, where α is defined as:
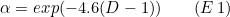
For a dimension D varying between 1 and 2, such a division would indeed be equivalent to a change of speed in a ratio of 100, the SMA being slowed down 100 times from its initial pace, in the extreme case of a dimension of 2.
This dimension D is a numerical approximation of the Box Dimension, itself an approximation of the Hausdorff dimension of the graph, which is properly the most mathematically precise fractal dimension. There is however, another dimension that can also be seen as a Box Dimension, but of another object relating to the process under study, and that Mandelbrot called the Trail Dimension [MAN97,pp.161&172).
For a Fractional Brownian Motion, we saw earlier that:
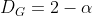
Where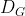
is what we have called so far the Fractal dimension, and α is the coefficient of the FBM (which is a different thing from the α of equation (E1)) . This latter is actually known as the Hurst-Holder exponent (or sometimes as simply the Hurst exponent, in memory of the British hydrologist whose studies of the long-term dependence of the Nile discharges, were inspirational to Mandelbrot works), and most often designed by H, I used α in reference to Falconer's book, but H seems more convenient from now on. We therefore have:
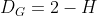
And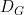
will now be known as the Graph Dimension. While the Trail Dimension will be defined as:
_________________________________________________________________________________________________________________
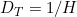
I-Interpretation of the Trail Dimension
It is easy to see that the Trail Dimension varies between 1 and ∞, for the coefficient H varying between 1 and 0. The first question is therefore how a "dimension" growing infinitely should be understood. In [MAN97], p.161, Mandelbrot wrote the following explanation:
My understanding of the above passage, in the general case of FBM (H varying between 0 and 1, while for WBM, H=1/2), is that the Trail dimension must be seen as an approximation of the number of dimensions in which the "real" process takes place (here it might be interesting to understand the term of "dimension" in a data-mining sense, rather than in a strict topological sense, prices are clearly the end-result of many independent processes, any of them with the potential of being chaotic in their own right), under the assumption that all the coordinates of the said process can be described as independent Fractional Brownian motions sharing the same Hurst exponent.
II-Slowing down the MA with the Trail Dimension
It is now possible to conceive of a formula for the coefficient α, using the Trail Dimension. The purpose of α is to slow down the MA from a reference speed when the Hurst exponent becomes very small, and also to accelerate it when this exponent becomes close to 1. The reference speed should be taken as the one used when the price varies in a gaussian way, that is when H is 1/2. So for such a value of H, we should have α=1.
If we then consider the following formula:
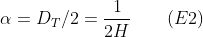
For a WBM, we have α=1. In addition, for a H tending towards 0, α tends towards infinity, and for H close to 1, α=1/2.
Comparing α from (E2)(red curve) with the inverse of α from (E1)(black curve)(we take the inverse in order to get a multiplicative factor rather than a dividing one to apply on the speed of the MA), we get the following graphs:
Or, for a more detailed view of their behavior below H=1/2:
Dividing the black curve by 10 in order to have an unchanged speed for the case of a WBM, we get the following:
For H varying from 0.5 to 0, we see that the α coming from (E1) varies almost linearly, for the same variation however, we know that the randomness increases in a rather non-linear fashion; a linear slowing down of the MA does not seem to reflect this properly. From this theoretical point of view, I therefore prefer the α given by equation (E2)(not to mention that it is much more simple).
III-Implementation of the FRASMA
I programmed the FRASMA(Fractally modified Simple Moving Average) in the MetaTrader platform. You may access and download freely this indicator, as well as use it on the metatrader 4 platform, at this address of the MQL4 Community.
Please, let me know your findings or any criticisms that can improve this indicator.
Meanwhile, here is a screenshot of three fractally modified MA, the Light Blue is a version of the FRAMA from Ehlers paper (modifying a EMA), the Yellow is a modification of a SMA using the following α inspired by Ehlers paper:
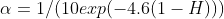
And the Red one is properly the FRASMA, using equation (E2).
Below is the fractal Graph Dimension. The period of reference for all original MA is 20.
IV-Conclusion
My purpose here is not to demonstrate that one indicator is better than another, since the quality of an indicator is relative to the manner one uses it. I believe that one must be acquainted intuitively with an indicator to use it productively, and it is for this reason that my preference is going to the FRASMA.
While one may just rely on direct practise to "understand" at an intuitive level a given indicator, I believe most of us can also profit from a theoretical understanding of them. My goal here is therefore to provide elements along these lines, for others to develop their own familiarity, and maybe provide me, in return, with some of their insights and experiences.
It is again naive to think that a trader, using technical analysis, can actually trade without some level of reliance on his intuition, and it is to totally miss the point of what the fractals tell us about the market to nourish expectations about a deterministic methodology to be successful as a trader, in other words, there is no Grail to be found in the first place. Nonetheless, to understand the technical tools one is using, can improve one's intuition, and the overall success of one's trading activity.
A modification, close to the one recommended by Ehlers, would be to merely divide the period of the SMA by the coefficient α, where α is defined as:
For a dimension D varying between 1 and 2, such a division would indeed be equivalent to a change of speed in a ratio of 100, the SMA being slowed down 100 times from its initial pace, in the extreme case of a dimension of 2.
This dimension D is a numerical approximation of the Box Dimension, itself an approximation of the Hausdorff dimension of the graph, which is properly the most mathematically precise fractal dimension. There is however, another dimension that can also be seen as a Box Dimension, but of another object relating to the process under study, and that Mandelbrot called the Trail Dimension [MAN97,pp.161&172).
For a Fractional Brownian Motion, we saw earlier that:
Where
And
_________________________________________________________________________________________________________________
I-Interpretation of the Trail Dimension
It is easy to see that the Trail Dimension varies between 1 and ∞, for the coefficient H varying between 1 and 0. The first question is therefore how a "dimension" growing infinitely should be understood. In [MAN97], p.161, Mandelbrot wrote the following explanation:
"First consider a Wiener Brownian motion in the plane. Its coordinates X(t) and Y(t) are independent Brownian motions. Therefore, if a 1-dimensional Brownian motion X(t) is combined with another independent 1-dimensional Brownian motion Y(t), the process X(t) becomes "embedded" into a 2-dimensional Brownian motion {X(t),Y(t)}. The value of the trail dimension:
is the fractal dimension of the three dimensional graph of coordinates t,X(t) and Y(t), and the projected "trail" of coordinates X(t) and Y(t). However, the dimension:
applies to the projected graphs of coordinates t and X(t) or t and Y(t)."
My understanding of the above passage, in the general case of FBM (H varying between 0 and 1, while for WBM, H=1/2), is that the Trail dimension must be seen as an approximation of the number of dimensions in which the "real" process takes place (here it might be interesting to understand the term of "dimension" in a data-mining sense, rather than in a strict topological sense, prices are clearly the end-result of many independent processes, any of them with the potential of being chaotic in their own right), under the assumption that all the coordinates of the said process can be described as independent Fractional Brownian motions sharing the same Hurst exponent.
II-Slowing down the MA with the Trail Dimension
It is now possible to conceive of a formula for the coefficient α, using the Trail Dimension. The purpose of α is to slow down the MA from a reference speed when the Hurst exponent becomes very small, and also to accelerate it when this exponent becomes close to 1. The reference speed should be taken as the one used when the price varies in a gaussian way, that is when H is 1/2. So for such a value of H, we should have α=1.
If we then consider the following formula:
For a WBM, we have α=1. In addition, for a H tending towards 0, α tends towards infinity, and for H close to 1, α=1/2.
Comparing α from (E2)(red curve) with the inverse of α from (E1)(black curve)(we take the inverse in order to get a multiplicative factor rather than a dividing one to apply on the speed of the MA), we get the following graphs:
Or, for a more detailed view of their behavior below H=1/2:
Dividing the black curve by 10 in order to have an unchanged speed for the case of a WBM, we get the following:
For H varying from 0.5 to 0, we see that the α coming from (E1) varies almost linearly, for the same variation however, we know that the randomness increases in a rather non-linear fashion; a linear slowing down of the MA does not seem to reflect this properly. From this theoretical point of view, I therefore prefer the α given by equation (E2)(not to mention that it is much more simple).
III-Implementation of the FRASMA
I programmed the FRASMA(Fractally modified Simple Moving Average) in the MetaTrader platform. You may access and download freely this indicator, as well as use it on the metatrader 4 platform, at this address of the MQL4 Community.
Please, let me know your findings or any criticisms that can improve this indicator.
Meanwhile, here is a screenshot of three fractally modified MA, the Light Blue is a version of the FRAMA from Ehlers paper (modifying a EMA), the Yellow is a modification of a SMA using the following α inspired by Ehlers paper:
And the Red one is properly the FRASMA, using equation (E2).
Below is the fractal Graph Dimension. The period of reference for all original MA is 20.
IV-Conclusion
My purpose here is not to demonstrate that one indicator is better than another, since the quality of an indicator is relative to the manner one uses it. I believe that one must be acquainted intuitively with an indicator to use it productively, and it is for this reason that my preference is going to the FRASMA.
While one may just rely on direct practise to "understand" at an intuitive level a given indicator, I believe most of us can also profit from a theoretical understanding of them. My goal here is therefore to provide elements along these lines, for others to develop their own familiarity, and maybe provide me, in return, with some of their insights and experiences.
It is again naive to think that a trader, using technical analysis, can actually trade without some level of reliance on his intuition, and it is to totally miss the point of what the fractals tell us about the market to nourish expectations about a deterministic methodology to be successful as a trader, in other words, there is no Grail to be found in the first place. Nonetheless, to understand the technical tools one is using, can improve one's intuition, and the overall success of one's trading activity.
Subscribe to:
Posts (Atom)